
分析 利用三角函数的最值,求出自变量x1,x2的值,然后判断选项即可.
解答 解:因为将函数f(x)=sin2x的周期为π,函数的图象向右平移φ(0<φ<$\frac{π}{2}$)个单位后得到函数g(x)的图象.
若对满足|f(x1)-g(x2)|=2的可知,两个函数的最大值与最小值的差为2,有|x1-x2|min=$\frac{π}{3}$,
不妨x1=$\frac{π}{4}$,x2=$\frac{7π}{12}$,即g(x)在x2=$\frac{7π}{12}$,取得最小值,sin(2×$\frac{7π}{12}$-2φ)=-1,此时φ=-$\frac{π}{6}$,不合题意,
x1=$\frac{3π}{4}$,x2=$\frac{5π}{12}$,即g(x)在x2=$\frac{5π}{12}$,取得最大值,sin(2×$\frac{5π}{12}$-2φ)=1,此时φ=$\frac{π}{6}$,满足题意.
故答案为:$\frac{π}{6}$.
点评 本题考查三角函数的图象平移,函数的最值以及函数的周期的应用,考查分析问题解决问题的能力,是好题,题目新颖.有一定难度,选择题,可以回代验证的方法快速解答.


科目:高中数学 来源: 题型:解答题
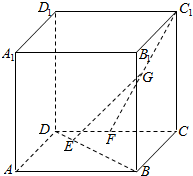 如图,已知正方体ABCD-A1B1C1D1的棱长为4,点E在线段BD上且|DE|=$\frac{1}{3}$|EB|,点F是CD的中点,G为C1F的中点,求EG的长.
如图,已知正方体ABCD-A1B1C1D1的棱长为4,点E在线段BD上且|DE|=$\frac{1}{3}$|EB|,点F是CD的中点,G为C1F的中点,求EG的长.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左、$\frac{π}{8}$单位 | B. | 向左、$\frac{π}{8}$单位 | C. | 向左、$\frac{3π}{8}$单位 | D. | 向右、$\frac{3π}{8}$单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com