
【题目】如图,在宽为![]() 的路边安装路灯,灯柱
的路边安装路灯,灯柱![]() 高为
高为![]() ,灯杆
,灯杆![]() 是半径为
是半径为![]() 的圆
的圆![]() 的一段劣弧.路灯采用锥形灯罩,灯罩顶
的一段劣弧.路灯采用锥形灯罩,灯罩顶![]() 到路面的距离为
到路面的距离为![]() ,到灯柱所在直线的距离为
,到灯柱所在直线的距离为![]() .设
.设![]() 为灯罩轴线与路面的交点,圆心
为灯罩轴线与路面的交点,圆心![]() 在线段
在线段![]() 上.
上.
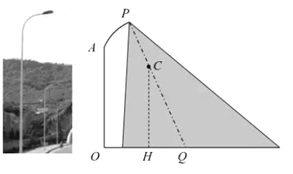
(1)当![]() 为何值时,点
为何值时,点![]() 恰好在路面中线上?
恰好在路面中线上?
(2)记圆心![]() 在路面上的射影为
在路面上的射影为![]() ,且
,且![]() 在线段
在线段![]() 上,求
上,求![]() 的最大值.
的最大值.
【答案】(1)当![]() 为
为![]() 时,点
时,点![]() 在路面中线上;(2)
在路面中线上;(2)![]()
【解析】
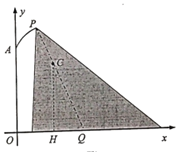
(1)以O为原点,以OA所在直线为y轴建立平面直角坐标系,求出PQ的方程,设C(a,b),根据CA=CP=r列方程组可得出a,b的值,从而求出r的值;
(2)用a表示出直线PQ的斜率,得出PQ的方程,求出Q的坐标,从而可得出|HQ|关于a的函数,根据a的范围和基本不等式得出|HQ|的最大值.
(1)以O为原点,以OA所在直线为y轴建立平面直角坐标系,则A(0,8),P(2,10),Q(7,0),
∴直线PQ的方程为2x+y﹣14=0.设C(a,b),则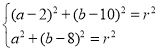 ,
,
两式相减得:a+b﹣10=0,又2a+b﹣14=0,解得a=4,b=6,
∴![]() .∴当
.∴当![]() 时,点Q恰好在路面中线上.
时,点Q恰好在路面中线上.
(2)由(1)知a+b﹣10=0,
当a=2时,灯罩轴线所在直线方程为x=2,此时HQ=0.
当a≠2时,灯罩轴线所在方程为:y﹣10=![]() (x﹣2),
(x﹣2),
令y=0可得x=12﹣![]() ,即Q(12﹣
,即Q(12﹣![]() ,0),
,0),
∵H在线段OQ上,∴12﹣![]() ≥a,解得2≤a≤10.
≥a,解得2≤a≤10.
∴|HQ|=12﹣![]() ﹣a=12﹣(
﹣a=12﹣(![]() +a)≤12﹣
+a)≤12﹣![]() =12﹣
=12﹣![]() ,
,
当且仅当![]() =a即a=
=a即a=![]() 时取等号.∴|HQ|的最大值为(12﹣
时取等号.∴|HQ|的最大值为(12﹣![]() )m.
)m.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求证:平面![]() 面
面![]() ;
;
(Ⅱ)过![]() 的平面交
的平面交![]() 于点
于点![]() ,若平面
,若平面![]() 把四面体
把四面体![]() 分成体积相等的两部分,求二面角
分成体积相等的两部分,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站退出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组
.现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
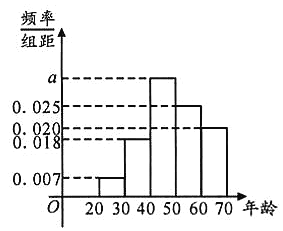
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(I)求出![]() 的值;
的值;
(II)求出这200人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(III)现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (其中
(其中![]() ).对于不相等的实数
).对于不相等的实数![]() ,
,![]() ,设
,设![]() ,
,![]() 下列说法正确的是( )
下列说法正确的是( )
A.对于任意不相等的实数![]() ,
,![]() ,都有
,都有![]() ;
;
B.对于任意的![]() 及任意不相等的实数
及任意不相等的实数![]() ,
,![]() ,都有
,都有![]() ;
;
C.对于任意的![]() ,存在不相等的实数
,存在不相等的实数![]() ,
,![]() ,使得
,使得![]() ;
;
D.对于任意的![]() ,存在不相等的实数
,存在不相等的实数![]() ,
,![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是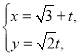 (
(![]() 为参数),曲线
为参数),曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,将曲线
,将曲线![]() 上的点向下平移1个单位,然后横坐标伸长为原来的2倍,纵坐标不变,得到曲线
上的点向下平移1个单位,然后横坐标伸长为原来的2倍,纵坐标不变,得到曲线![]() .
.
(1)求曲线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 和曲线
和曲线![]() 相交于
相交于![]() 两点,求三角形
两点,求三角形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司给年龄在![]() 岁的民众提供某种疾病的一年期医疗保险,现从
岁的民众提供某种疾病的一年期医疗保险,现从![]() 名参保人员中随机抽取
名参保人员中随机抽取![]() 名作为样本进行分析,按年龄段
名作为样本进行分析,按年龄段![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分成了五组,其频率分布直方图如下图所示,参保年龄与每人每年应交纳的保费如下表所示.
分成了五组,其频率分布直方图如下图所示,参保年龄与每人每年应交纳的保费如下表所示.
年龄(单位:岁) |
|
|
|
|
|
保费(单位:元) |
|
|
|
|
|
(1)求频率分布直方图中实数![]() 的值,并求出该样本年龄的中位数;
的值,并求出该样本年龄的中位数;
(2)现分别在年龄段![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中各选出
中各选出![]() 人共
人共![]() 人进行回访.若从这
人进行回访.若从这![]() 人中随机选出
人中随机选出![]() 人,求这
人,求这![]() 人所交保费之和大于
人所交保费之和大于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年双十一落下帷幕,天猫交易额定格在268(单位:十亿元)人民币(下同),再创新高,比去年218(十亿元)多了50(十亿元).这些数字的背后,除了是消费者买买买的表现,更是购物车里中国新消费的奇迹,为了研究历年销售额的变化趋势,一机构统计了2010年到2019年天猫双十一的销售额数据y(单位:十亿元),绘制如表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
编号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
销售额y | 0.9 | 8.7 | 22.4 | 41 | 65 | 94 | 132.5 | 172.5 | 218 | 268 |
根据以上数据绘制散点图,如图所示
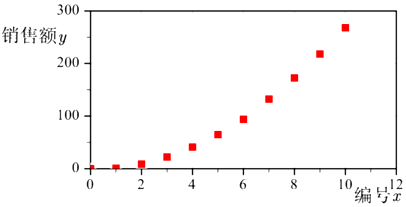
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为销售额
哪一个适宜作为销售额![]() 关于
关于![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及如表中的数据,建立![]() 关于
关于![]() 的回归方程,并预测2020年天猫双十一销售额;(注:数据保留小数点后一位)
的回归方程,并预测2020年天猫双十一销售额;(注:数据保留小数点后一位)
(3)把销售超过100(十亿元)的年份叫“畅销年”,把销售额超过200(十亿元)的年份叫“狂欢年”,从2010年到2019年这十年的“畅销年”中任取2个,求至少取到一个“狂欢年”的概率.
参考数据:![]()
|
|
|
|
|
|
参考公式:
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别
的斜率和截距的最小二乘估计公式分别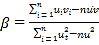 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com