
| A. | $2\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | 8 | D. | 4 |
分析 先根据抛物线方程求得抛物线的焦点坐标,进而根据点斜式求得直线的方程与抛物线方程联立,消去y,根据韦达定理求得x1+x2=的值,进而根据抛物线的定义可知|AB|=x1+$\frac{p}{2}$+x2+$\frac{p}{2}$,求得答案.
解答 解:抛物线的参数方程为$\left\{{\begin{array}{l}{x=4{t^2}}\\{y=4t}\end{array}}\right.$,普通方程为y2=4x,抛物线焦点为(1,0),且斜率为1,
则直线方程为y=x-1,代入抛物线方程y2=4x得
x2-6x+1=0,设A(x1,y1),B(x2,y2)
∴x1+x2=6
根据抛物线的定义可知|AB|=x1+$\frac{p}{2}$+x2+$\frac{p}{2}$
=x1+x2+p=6+2=8,
故选C.
点评 本题主要考查了直线与圆锥曲线的关系,抛物线的简单性质.对学生基础知识的综合考查.关键是:将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根与系数的关系,利用弦长公式即可求得|AB|值,从而解决问题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河南省商丘市高一文下学期期末考数学试卷(解析版) 题型:填空题
O是面α上一定点,A,B,C是面α上△ABC的三个顶点,∠B,∠C分别是边AC,AB的对角.以下命题正确的是________.(把你认为正确的序号全部写上)
①动点P满足 ,则△ABC的外心一定在满足条件的P点集合中;
,则△ABC的外心一定在满足条件的P点集合中;
②动点P满足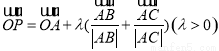 ,则△ABC的内心一定在满足条件的P点集合中;
,则△ABC的内心一定在满足条件的P点集合中;
③动点P满足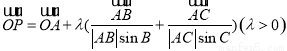 ,则△ABC的重心一定在满足条件的P点集合中;
,则△ABC的重心一定在满足条件的P点集合中;
④动点P满足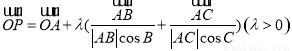 ,则△ABC的垂心一定在满足条件的P点集合中.
,则△ABC的垂心一定在满足条件的P点集合中.
⑤动点P满足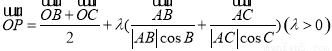 ,则△ABC的外心一定在满足条件的P点集合中.
,则△ABC的外心一定在满足条件的P点集合中.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com