练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．已知函数f（x）=$\left\{\begin{array}{l}\frac{1}{x^2}，x＜1\\{log_2}（{x+4}），x≥1\end{array}$，则$f（f（\frac{1}{2}））$=（　　）
    A．2B．3C．4D．8

    分析 先求出f（$\frac{1}{2}$）=$\frac{1}{（\frac{1}{2}）^{2}}$=4，从而$f（f（\frac{1}{2}））$=f（4），由此能求出结果．

    解答 解：∵函数f（x）=$\left\{\begin{array}{l}\frac{1}{x^2}，x＜1\\{log_2}（{x+4}），x≥1\end{array}$，
    ∴f（$\frac{1}{2}$）=$\frac{1}{（\frac{1}{2}）^{2}}$=4，
    $f（f（\frac{1}{2}））$=f（4）=log28=3．
    故选：B．

    点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

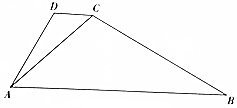    5．如图，在梯形ABCD中，AB∥CD，∠DAC=30°，∠CAB=45°，CD=$\sqrt{6}$-$\sqrt{2}$．
    （Ⅰ）求AD的长；
    （Ⅱ）若BC=$\sqrt{10}$，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知向量|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=3，|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{7}$，那么|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{19}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知对数函数f（x）=logax（a＞0，且a≠1）的图象经过点（4，2）．
    （1）求实数a的值；
    （2）如果f（x+1）＜0，求实数x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知抛物线的参数方程为$\left\{{\begin{array}{l}{x=4{t^2}}\\{y=4t}\end{array}}\right.$，若斜率为1的直线经过抛物线的焦点，且与抛物线相交于A，B两点，则线段AB的长为（　　）
    A．$2\sqrt{2}$B．$4\sqrt{2}$C．8D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．若f（x）=$\frac{1}{{{2^x}+2}}$+a是奇函数，则a=-$\frac{1}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．若$\overrightarrow a=（-3，2，5），\overrightarrow b=（1，-3，0），\overrightarrow c=（7，-2，1）$，则$（\overrightarrow a+\overrightarrow b）•\overrightarrow c$=-7．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．设函数f（x）=$\left\{\begin{array}{l}{-{x}^{2}+4x+4，x＜k}\\{4x+3，x≥k}\end{array}\right.$是（-∞，+∞）上的增函数，那么实数k的取值范围为（-∞，-1]∪[1，2]．

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年河南省商丘市高一文下学期期末考数学试卷（解析版） 题型：选择题

    四名同学根据各自的样本数据研究变量x，y之间的相关关系，并求得回归直线方程，分别得到以下四个结论：①y与x负相关且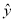＝2．347x－6．423；②y与x负相关且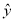＝－3．476x＋5．648；③y与x正相关且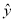＝5．437x＋8．493；④y与x正相关且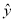＝－4．326x－4．578．其中一定不正确的结论的序号是（ ）

    A．①② B．②③ C．③④ D．①④

    查看答案和解析>>

    同步练习册答案