
分析 根据函数的解析式、一元二次函数的单调性、函数单调性的性质,列出不等式组,求出实数k的取值范围.
解答 解:∵f(x)=$\left\{\begin{array}{l}{-{x}^{2}+4x+4,x<k}\\{4x+3,x≥k}\end{array}\right.$是(-∞,+∞)上的增函数,
∴$\left\{\begin{array}{l}{k≤2}\\{{-k}^{2}+4k+4≤4k+3}\end{array}\right.$,解得k≤-1或1≤k≤2,
则实数k的取值范围是(-∞,-1]∪[1,2],
故答案为:(-∞,-1]∪[1,2].
点评 本题考查函数单调性的性质,以及一元二次函数的单调性,注意端点处函数的大小关系.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
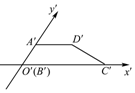 已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是( )
已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是( )| A. | $\sqrt{5}$ | B. | $2\sqrt{2}$ | C. | $2\sqrt{5}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年湖北省仙桃市高一下学期期末考试数学试卷(解析版) 题型:选择题
完成一项装修工程,请木工共需付工资每人500元,请瓦工共需付工资每人400元,现有工人工资预算20000元,设木工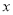 人,瓦工
人,瓦工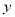 人,则工人满足的关系式是( )
人,则工人满足的关系式是( )
A.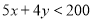 B.
B.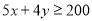
C.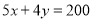 D.
D.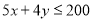
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河南省商丘市高一理下学期期末考数学试卷(解析版) 题型:选择题
连掷两次骰子分别得到点数m,n,则向量(m,n)与向量(-1,1)的夹角θ>90°的概率是( )
A.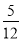 B.
B.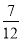 C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com