
分析 (Ⅰ)求得f(x)的对称轴方程,可得f(x)在[0,1]递减,在[1,3]上递增,即可得到最值,解方程可得a,b的值;
(Ⅱ)求出函数|f(x)-2x|的值域,即可得到关于t的不等式组,解得即可,
(Ⅲ)设2x=m,则m∈[2,4],分离参数,构造函数,利用导数求出函数的最值即可.
解答 解:(Ⅰ)函数f(x)=ax2-2ax+1+b=a(x-1)2+1+b-a,
∵a>0,开口向上,对称轴x=1,
∴f(x)在[0,1]递减,在[1,3]上递增,
∴f(x)min=f(1)=a-2a+1+b=1,f(x)max=f(3)=9a-6a+1+b=5,
∴a=1,b=1,
(Ⅱ)由(Ⅰ)可得f(x)=x2-2x+2,
∴f(x)-2x=x2-4x+2=(x-2)2-2,
对称轴x=2,
∴f(x)-2x在[-1,2]递减,在[2,3]上递增,
∴最小值为-2,最大值为7,
∴|f(x)-2x|∈[0,7],
∵方程|f(x)-2x|=t2-2t-8有解,
∴0≤t2-2t-8≤7,
解得-3≤t≤-2或4≤t≤5,
故t的范围为[-3,-2]∪[4,5],
(Ⅲ)g(x)=$\frac{f(x)}{x}$=x+$\frac{2}{x}$-2,
设2x=m,
∵x∈[1,2],
∴m∈[2,4],
∵$g({2^x})+k•\frac{2}{2^x}-k≥0$在x∈[1,2]上恒成立,
∴m+$\frac{2k}{m}$-k≥0.在m∈[2,4]上恒成立,
∴当m=2时,2≥0恒成立,
当m≠2时,k≤$\frac{{m}^{2}}{m-2}$,
设h(m)=$\frac{{m}^{2}}{m-2}$
∴h′(m)=$\frac{m(m-4)}{(m-2)^{2}}$≤0,在[2,4]上恒成立,
∴h(m)在[2,4]上单调递减,
∴h(m)min=h(4)=8,
∴k≤8
点评 本题考查了二次函数的性质以及参数的取值范围和恒成立的问题,属于中档题


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
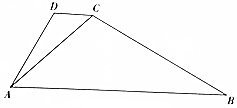 如图,在梯形ABCD中,AB∥CD,∠DAC=30°,∠CAB=45°,CD=$\sqrt{6}$-$\sqrt{2}$.
如图,在梯形ABCD中,AB∥CD,∠DAC=30°,∠CAB=45°,CD=$\sqrt{6}$-$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com