
科目:高中数学 来源: 题型:选择题
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 蒜台 | 4吨 | 1.2万元 | 0.55万元 |
| 花菜 | 6吨 | 0.9万元 | 0.3万元 |
| A. | 50万 | B. | 48万 | C. | 47万 | D. | 45万 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 10 | C. | -10 | D. | -20 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
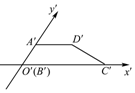 已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是( )
已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是( )| A. | $\sqrt{5}$ | B. | $2\sqrt{2}$ | C. | $2\sqrt{5}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年湖北省仙桃市高一下学期期末考试数学试卷(解析版) 题型:选择题
完成一项装修工程,请木工共需付工资每人500元,请瓦工共需付工资每人400元,现有工人工资预算20000元,设木工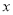 人,瓦工
人,瓦工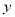 人,则工人满足的关系式是( )
人,则工人满足的关系式是( )
A.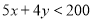 B.
B.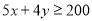
C.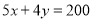 D.
D.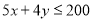
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com