
分析 根据题意,由函数的奇偶性与单调性分析可得f(x)在[-2,0]上单调递减,进而分析可得$\left\{\begin{array}{l}-2≤1-m≤2①\\-2≤1+m≤2②\\|{1-m}|<|{1+m}|③\end{array}\right.$,解可得m的取值范围,即可得答案.
解答 解:∵f(x)是[-2,2]上的偶函数,
且在[-2,0]上单调递减,
∴f(x)在[0,2]上单调递增,
由f(1-m)<f(1+m)得$\left\{\begin{array}{l}-2≤1-m≤2①\\-2≤1+m≤2②\\|{1-m}|<|{1+m}|③\end{array}\right.$
解①得-3≤m≤1,
解②得-1≤m≤3,
由①②得-1≤m≤1,
则③可化简为(1-m)2<(1+m)2,
得m>0,
综上得m的范围为0<m≤1.
点评 本题考查函数的奇偶性与单调性的综合应用,关键是综合利用函数的奇偶性与单调性,得到关于m的不等式组.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | 8 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2300元 | B. | 2800元 | C. | 2400元 | D. | 2000元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| A区域 | 86 91 95 100 103 112 123 |
| B区域 | 84 92 93 95 95 97 98 106 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河南省商丘市高一文下学期期末考数学试卷(解析版) 题型:选择题
连掷两次骰子分别得到点数m,n,则向量(m,n)与向量(-1,1)的夹角θ>90°的概率是( )
A.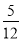 B.
B. C.
C.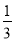 D.
D.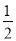
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com