
在直角坐标系xOy中,中心在原点O,焦点在x轴上的椭圆C上的点(2 ,1)到两焦点的距离之和为4
,1)到两焦点的距离之和为4 .
.
(1)求椭圆C的方程;
(2)过椭圆C的右焦点F作直线l与椭圆C分别交于A,B两点,其中点A在x轴下方,且 =3
=3 .求过O,A,B三点的圆的方程.
.求过O,A,B三点的圆的方程.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用21练习卷(解析版) 题型:填空题
从长度分别为2,3,4,5的四条线段中任意取出三条,则以这三条线段为边可以构成三角形的概率是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用18练习卷(解析版) 题型:解答题
已知(1+x)n=a0+a1(x-1)+a2(x-1)2+…+an(x-1)n(n∈N*).
(1)求a0及Sn=a1+a2+a3+…+an;
(2)试比较Sn与(n-2)2n+2n2的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用15练习卷(解析版) 题型:解答题
已知曲线C1: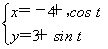 (t为参数),C2:
(t为参数),C2:
(θ为参数).
(1)化C1、C2的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C1上的点P对应的参数为t= ,Q为C2上的动点,求PQ中点M到直线C3:
,Q为C2上的动点,求PQ中点M到直线C3: (t为参数)距离的最小值.
(t为参数)距离的最小值.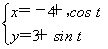
解
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用13练习卷(解析版) 题型:填空题
设F1是椭圆 +y2=1的左焦点,O为坐标原点,点P在椭圆上,则
+y2=1的左焦点,O为坐标原点,点P在椭圆上,则 ·
· 的最大值为________.
的最大值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用12练习卷(解析版) 题型:填空题
设椭圆C∶ =1(a>b>0)恒过定点A(1,2),则椭圆的中心到准线的距离的最小值________.
=1(a>b>0)恒过定点A(1,2),则椭圆的中心到准线的距离的最小值________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用11练习卷(解析版) 题型:填空题
已知直线x-y+a=0与圆x2+y2=1交于A、B两点,且向量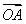 、
、 满足|
满足|  +
+ |=|
|=|  -
- |,其中O为坐标原点,则实数a的值为______.
|,其中O为坐标原点,则实数a的值为______.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试选择填空限时训练3练习卷(解析版) 题型:选择题
已知函数f(x)的导函数为f′(x),且满足f(x)=2xf′(e)+ln x,则f′(e)=( )
A.1 B.-1 C.-e-1 D.-e
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com