
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | -3 | D. | 1 |
分析 由题意,$\overrightarrow{CD}$=2$\overrightarrow{DB}$,可得$\frac{2}{3}\overrightarrow{CB}=\overrightarrow{CD}$,$\overrightarrow{CB}=3\overrightarrow{DB}$,根据向量的三角形法则进行加减运算,找到关系,即可求r+s的值.
解答 解:由题意,$\overrightarrow{CD}$=2$\overrightarrow{DB}$,可得$\frac{2}{3}\overrightarrow{CB}=\overrightarrow{CD}$,$\overrightarrow{CB}=3\overrightarrow{DB}$,
∵$\overrightarrow{CB}=\overrightarrow{AB}-\overrightarrow{AC}$
∴$\frac{2}{3}\overrightarrow{AB}-\frac{2}{3}\overrightarrow{AC}=\overrightarrow{CD}$,
又∵$\overrightarrow{AD}=\overrightarrow{AC}+\overrightarrow{CD}$,
则:$\overrightarrow{AD}=\overrightarrow{AC}+\frac{2}{3}\overrightarrow{AB}-\frac{2}{3}\overrightarrow{AC}$=$\frac{1}{3}\overrightarrow{AC}+\frac{2}{3}\overrightarrow{AB}$
所以:r=$\frac{2}{3}$,s=$\frac{1}{3}$
那么:r+s=$\frac{1}{3}+\frac{2}{3}$=1
故选:D.
点评 本题考查了平面向量的线性运算的应用及平面向量基本定理的应用.注意平面向量加法法则的合理运用.属于基础题.


科目:高中数学 来源: 题型:解答题
 小明到他父亲的木工房,看到一个棱长为50cm的立方体工件(如图),从立方体的前后、左右、上下看,都有且仅有两个相通的正方形孔,请你算一算,这个立方体剩下的体积是多少?
小明到他父亲的木工房,看到一个棱长为50cm的立方体工件(如图),从立方体的前后、左右、上下看,都有且仅有两个相通的正方形孔,请你算一算,这个立方体剩下的体积是多少?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 优秀 | 非优秀 | 合计 | |
| 甲班 | 10 | 50 | 60 |
| 乙班 | 20 | 30 | 50 |
| 合计 | 30 | 80 | 110 |
| K2≥k | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| A. | 90% | B. | 95% | C. | 99% | D. | 99.9% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1000 | B. | 600 | C. | 550 | D. | 500 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
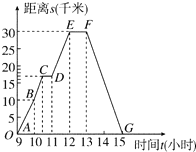 如图,该曲线表示一人骑自行车离家的距离与时间的关系.骑车者9时离开家,15时回家.根据这个曲线图,请你回答下列问题:
如图,该曲线表示一人骑自行车离家的距离与时间的关系.骑车者9时离开家,15时回家.根据这个曲线图,请你回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com