
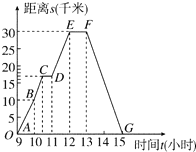
 ��ͼ�������߱�ʾһ�������г���ҵľ�����ʱ��Ĺ�ϵ���ﳵ��9ʱ�뿪�ң�15ʱ�ؼң������������ͼ������ش��������⣺
��ͼ�������߱�ʾһ�������г���ҵľ�����ʱ��Ĺ�ϵ���ﳵ��9ʱ�뿪�ң�15ʱ�ؼң������������ͼ������ش��������⣺���� ���ݺ�����ͼ��������������
��� �⣺��1��������������Զ�ĵط���12ʱ�����30ǧ�ף�
��2����һ����Ϣʱ��Ϊ10��30����Ϣʱ��Ϊ30���ӣ�
��3����һ����Ϣʱ���17ǧ�ף�
��4��11��00��12��00������30-17=13ǧ�ף�
��5��9��00-10��00��ƽ���ٶ�Ϊ$\frac{10}{1}$=10ǧ��/ʱ��
10��00-10��30��ƽ���ٶ�Ϊ$\frac{17-10}{0.5}$=14ǧ��/ʱ��
��6����12��00-13��00ֹͣǰ������Ϣ����ͣ�
���� ���⿼���˺�����ͼ������壬���ڻ����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ض�ֻ�����㹲�� | B�� | �������㲻���� | ||
| C�� | ���������㹲�� | D�� | �����������㹲�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{3}$ | B�� | $\frac{4}{3}$ | C�� | -3 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 4 | C�� | $\frac{1}{2}$ | D�� | $-\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-1�� | B�� | ��-�ޣ�2�� | C�� | ��0��2�� | D�� | [0��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2��2�� | B�� | ��0��2�� | C�� | ��-1��1�� | D�� | ��$\frac{1}{2}$��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com