
分析 函数f(x)是一个复合函数,f(x)的值域为[0.+∞),外层函数是定义域内的增函数,只需保证内层函数(m2-1)x2-(1-m)x+1值域能取到[0.+∞)即可实数m的取值范围.
解答 解:由题意:函数f(x)=$\sqrt{({m^2}-1){x^2}-(1-m)x+1}$是一个复合函数,设f(x)=${u}^{\frac{1}{2}}$(u≥0)值域为[0.+∞),则u=(m2-1)x2-(1-m)x+1的值域能取到[0.+∞)即umin≤0可满足题意.
∴m2-1>0.解得:m>1或m<-1.
∵u=(m2-1)x2-(1-m)x+1,开口向上,对称轴x=$-\frac{1}{2(m+1)}$,
那么:${u}_{min}=({m}^{2}-1)(\frac{1}{2(m+1)})^{2}+(1-m)(\frac{1}{2(m+1)})+1$≤0
整理得:3m2+8m+5≤0
解得:-$\frac{5}{3}$≤m≤-1
当m=-1时,u=(m2-1)x2-(1-m)x+1=-2x+1,值域能取到[0.+∞),故m=-1成立.
所以:-$\frac{5}{3}$≤m≤-1.
故实数m的取值范围为[-$\frac{5}{3}$,-1].
点评 本题考查了复合函数的值域问题,通过值域来求参数.计算量大,化简繁琐,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1000 | B. | 600 | C. | 550 | D. | 500 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
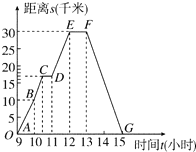 如图,该曲线表示一人骑自行车离家的距离与时间的关系.骑车者9时离开家,15时回家.根据这个曲线图,请你回答下列问题:
如图,该曲线表示一人骑自行车离家的距离与时间的关系.骑车者9时离开家,15时回家.根据这个曲线图,请你回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 8$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?a∈R,方程ax2+2x+1=0无负实根 | B. | ?a∈R,方程ax2+2x+1=0有正实根 | ||
| C. | ?a∈R,方程ax2+2x+1=0有正实根 | D. | ?a∈R,方程ax2+2x+1=0无负实根 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
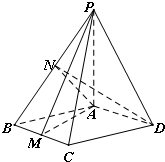 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=$\sqrt{6}$,四边形ABCD是边长为2的菱形,∠ABC=60°,M,N分别为BC和PB的中点..
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=$\sqrt{6}$,四边形ABCD是边长为2的菱形,∠ABC=60°,M,N分别为BC和PB的中点..查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com