
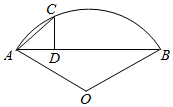
 如图,若$\widehat{ACB}$是半径为r的圆的弓形,弦AB长为$\sqrt{2}$r,C为劣弧AB上的一点,CD⊥AB于D,当点C在什么位置时,△ACD的面积最大,并求这个最大面积.
如图,若$\widehat{ACB}$是半径为r的圆的弓形,弦AB长为$\sqrt{2}$r,C为劣弧AB上的一点,CD⊥AB于D,当点C在什么位置时,△ACD的面积最大,并求这个最大面积. 分析 先表示出△ACD的面积,再用基本不等式求出最大面积.
解答 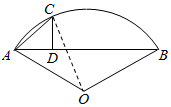 解:∵$\widehat{ACB}$是半径为r的圆的弓形,弦AB长为$\sqrt{2}$r,
解:∵$\widehat{ACB}$是半径为r的圆的弓形,弦AB长为$\sqrt{2}$r,
∴∠AOB=90°.
连接OC,设∠CAB=α,则∠BOC=2α,∠AOC=90°-2α,
∴AC=2rsin(45°-α),
∴AD=ACcosα,
∴△ACD的面积S=$\frac{1}{2}×AC×AD×sinα$=r2sin2(45°-α)sin2α
=$\frac{{r}^{2}}{2}×(1-sin2α)sin2α$≤$\frac{{r}^{2}}{2}×(\frac{1}{2})^{2}$=$\frac{{r}^{2}}{8}$.
当且仅当1-sin2α=sin2α,即sin2α=$\frac{1}{2}$,
∴α=$\frac{π}{12}$时,△ACD的面积最大,最大面积为$\frac{{r}^{2}}{8}$.
点评 本题考查三角形面积的计算,考查三角函数知识,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12种 | B. | 36种 | C. | 48种 | D. | 72种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com