
| A�� | $\sqrt{2}$ | B�� | $\sqrt{3}$ | C�� | 1 | D�� | -1 |
���� ���������������������ʣ�������ƽ����Ϊģ��ƽ��������$\overrightarrow{a}$��$\overrightarrow{b}$�����ϵ�ͶӰ������㼴�����
��� �⣺��|$\overrightarrow{a}$|=2|$\overrightarrow{b}$|=2��|$\overrightarrow{a}$-4$\overrightarrow{b}$|=2$\sqrt{7}$��
��|$\overrightarrow{a}$-4$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+16|$\overrightarrow{b}$|2-8$\overrightarrow{a}$•$\overrightarrow{b}$=28��
��$\overrightarrow{a}$•$\overrightarrow{b}$=-1��
����$\overrightarrow{a}$��$\overrightarrow{b}$�����ϵ�ͶӰΪ$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$=-1��
��ѡ��D��
���� ���⿼���������������Ķ�������ʣ���Ҫ����������ƽ����Ϊģ��ƽ�����Լ�������ͶӰ���������е��⣮


 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
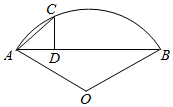 ��ͼ����$\widehat{ACB}$�ǰ뾶Ϊr��Բ�Ĺ��Σ���AB��Ϊ$\sqrt{2}$r��CΪ�ӻ�AB�ϵ�һ�㣬CD��AB��D������C��ʲôλ��ʱ����ACD���������������������
��ͼ����$\widehat{ACB}$�ǰ뾶Ϊr��Բ�Ĺ��Σ���AB��Ϊ$\sqrt{2}$r��CΪ�ӻ�AB�ϵ�һ�㣬CD��AB��D������C��ʲôλ��ʱ����ACD����������������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 5 | C�� | 4 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{{m}^{2}}$ | B�� | $\frac{1}{m}$ | C�� | 2m | D�� | $\frac{2}{m}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com