
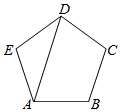
分析 设出边长,利用向量的数量积公式化简求解即可.
解答 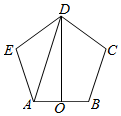 解:设正五边形ABCDE的边长为a.$|\overrightarrow{AD}|cos<\overrightarrow{AB},\overrightarrow{AD}>$=$|\overrightarrow{AO}|=\frac{1}{2}|\overrightarrow{AB}|$.
解:设正五边形ABCDE的边长为a.$|\overrightarrow{AD}|cos<\overrightarrow{AB},\overrightarrow{AD}>$=$|\overrightarrow{AO}|=\frac{1}{2}|\overrightarrow{AB}|$.
∵$\overrightarrow{AB}$•$\overrightarrow{AD}$=8,可得:|$\overrightarrow{AB}$|•|$\overrightarrow{AD}$|cos$<\overrightarrow{AB},\overrightarrow{AD}>$=8,即$\frac{1}{2}|\overrightarrow{AB}||\overrightarrow{AB}|=8$,即$\frac{1}{2}{a}^{2}=8$,解得a=4.
故答案为:4.
点评 本题考查平面向量的数量积的应用,考查计算能力.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
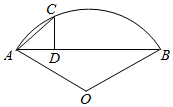 如图,若$\widehat{ACB}$是半径为r的圆的弓形,弦AB长为$\sqrt{2}$r,C为劣弧AB上的一点,CD⊥AB于D,当点C在什么位置时,△ACD的面积最大,并求这个最大面积.
如图,若$\widehat{ACB}$是半径为r的圆的弓形,弦AB长为$\sqrt{2}$r,C为劣弧AB上的一点,CD⊥AB于D,当点C在什么位置时,△ACD的面积最大,并求这个最大面积.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{c}$+$\overrightarrow{b}$ | B. | $\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{c}$+$\frac{1}{2}$$\overrightarrow{b}$ | C. | $\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{c}$-$\frac{1}{2}$$\overrightarrow{b}$ | D. | $\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{c}$-$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{m}^{2}}$ | B. | $\frac{1}{m}$ | C. | 2m | D. | $\frac{2}{m}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{2}$,+∞) | B. | (1,$\frac{1}{e}$) | C. | [e,+∞) | D. | (e,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com