
分析 (1)直接利用函数的单调性的定义证明即可.
(2)利用函数的单调性,直接求解函数的最值即可.
解答 解:(1)f(x)在[2,5]上是增函数.
理由:在[2,5]上任取两个数x1<x2,
则有$f({x_1})-f({x_2})=\frac{{3{x_1}}}{{{x_1}+1}}-\frac{{3{x_2}}}{{{x_2}+1}}$=$\frac{{3({x_1}-{x_2})}}{{({x_1}+1)({x_2}+1)}}$<0,
所以f(x)在[2,5]上是增函数.
(2)由(1)可知函数是增函数,
f(x)在区间[2,5]上的最大值f(2)=2;最小值f(5)=$\frac{5}{2}$.
点评 本题考查函数的单调性以及函数的最值的求法,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
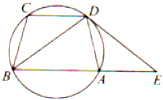 如图,已知圆上的四点A、B、C、D,CD∥AB,过点D的圆的切线DE与BA的延长线交于E点.
如图,已知圆上的四点A、B、C、D,CD∥AB,过点D的圆的切线DE与BA的延长线交于E点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | 2017 | C. | 1007 | D. | 1008 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+2y-5=0 | B. | 2x-y+5=0 | C. | x-2y+5=0 | D. | 2x+y-5=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com