练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法，其理论依据是：设实数的不足近似值和过剩近似值分别为和，则是的更为精确的不足近似值或过剩近似值.我们知道，若令，则第一次用“调日法”后得是的更为精确的过剩近似值，即，若每次都取最简分数，那么第四次用“调日法”后可得的近似分数为（ ）

    A.B.C.D.

    【答案】D

    【解析】

    根据“调日法”的循环规律求解.

    第一次用“调日法”后得是的更为精确的过剩近似值，即，

    第二次用“调日法”后得是的更为精确的过剩近似值，即

    ，

    第三次用“调日法”后得是的更为精确的过剩近似值，即

    ，

    第四次用“调日法”后得是的更为精确的过剩近似值，即

    故第四次用“调日法”后可得的近似分数为

    故选：D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】近年来，共享单车在我国各城市迅猛发展，为人们的出行提供了便利，但也给城市的交通管理带来了一些困难，为掌握共享单车在省的发展情况，某调查机构从该省抽取了5个城市，并统计了共享单车的指标和指标，数据如下表所示：

    城市1

    城市2

    城市3

    城市4

    城市5

    指标

    2

    4

    5

    6

    8

    指标

    3

    4

    4

    4

    5

    （1）试求与间的相关系数，并说明与是否具有较强的线性相关关系（若，则认为与具有较强的线性相关关系，否则认为没有较强的线性相关关系）.

    （2）建立关于的回归方程，并预测当指标为7时，指标的估计值.

    （3）若某城市的共享单车指标在区间的右侧，则认为该城市共享单车数量过多，对城市的交通管理有较大的影响交通管理部门将进行治理，直至指标在区间内现已知省某城市共享单车的指标为13，则该城市的交通管理部门是否需要进行治理？试说明理由.

    参考公式：回归直线中斜率和截距的最小二乘估计分别为

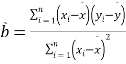    ，，相关系数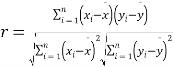

    参考数据：，，.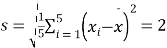

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C：（）的一个焦点与抛物线的焦点相同，，为椭圆的左、右焦点，M为椭圆上任意一点，若的面积最大值为1.

    （1）求椭圆C的方程；

    （2）设不过原点的直线l：与椭圆C交于不同的两点A、B，若直线l的斜率是直线、斜率的等比中项，求面积的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线的极坐标方程是,以极点为平面直角坐标系的原点,极轴为轴的正半轴，建立平面直角坐标系,曲线C的参数方程是,（为参数）.

    （1）求直线被曲线C截得的弦长；

    （2）从极点作曲线C的弦,求各弦中点轨迹的极坐标方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列的前项和为，满足，．数列满足，，且．

    （1）求数列和的通项公式；

    （2）若，数列的前项和为，对任意的，都有，求实数的取值范围；

    （3）是否存在正整数，，使，，（）成等差数列，若存在，求出所有满足条件的，，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】

    已知函数f（x）=，其中a>0.

    （Ⅰ）若a=1，求曲线y=f（x）在点（2，f（2））处的切线方程；

    （Ⅱ）若在区间上，f（x）>0恒成立，求a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分14分）已知函数f（x）＝－2lnx＋x2－2ax＋a2，其中a>0.

    （Ⅰ）设g（x）为f（x）的导函数，讨论g（x）的单调性；

    （Ⅱ）证明：存在a∈（0，1），使得f（x）≥0恒成立，且f（x）＝0在区间（1，＋∞）内有唯一解.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥的底面为矩形，平面平面，点在线段上，且平面.

    （1）求证：平面；

    （2）若点是线段上靠近的三等分点，点在线段上，且平面，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，已知椭圆C：（） 经过点，设椭圆C的左顶点为A，右焦点为F，右准线于x轴交于点M，且F为线段AM的中点，

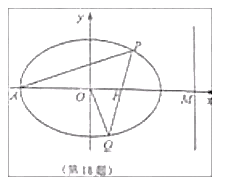
    （1）求椭圆的标准方程；

    （2）若过点A的直线l与椭圆C交于另一点P（P在x轴上方），直线PF与椭圆C相交于另一点Q，且直线l与OQ垂直，求直线PQ的斜率.

    查看答案和解析>>

    同步练习册答案