Question

9．设函数f（x）=|log₂x+ax+b|（a＞0）在区间[t，t+2]（t＞0）上的最大值为M_t（a，b），若{b|M_t（a，b）≥1+a}=R，则实数t的最大值为$\frac{2}{3}$．

Answer 1

分析 由题意：f（x）=|log₂x+ax+b|（a＞0）在区间[t，t+2]（t为正数）上的最大值为M_t（a，b），转化为
f（x）_max={f（t），f（t+2）}，当f（t）=f（t+2）时，则有：-（log₂t+at+b）=log₂（t+2）+a（t+2）+b，可得：b=$\frac{lo{g}_{2}（t+2）+lo{g}_{2}t+2a（t+1）}{-2}$，f（x）_max＞f（t）或f（x）_max＞f（t+2）因此只需要f（t）≥1+a，即可得出．

解答 解：由题意：f（x）=|log₂x+ax+b|（a＞0）在区间[t，t+2]（t为正数）上的最大值为M_t（a，b），转化为
f（x）_max={f（t），f（t+2）}，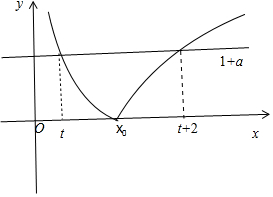
当f（t）=f（t+2）时，
则有：-（log₂t+at+b）=log₂（t+2）+a（t+2）+b
那么：b=$\frac{lo{g}_{2}（t+2）+lo{g}_{2}t+2a（t+1）}{-2}$…①
当t＞x₀或t＜x₀时，
f（x）_max＞f（t）或f（x）_max＞f（t+2）
∴只需要f（t）≥1+a，
即：-（log₂t+at+b）≥1+a
得：b≤-log₂t-at-1-a…②
把①式代入②，
得：$\frac{lo{g}_{2}（t+2）+lo{g}_{2}t+2a（t+1）}{-2}$≤-log₂t-at-1-a，
化为：$lo{g}_{2}\frac{t+2}{t}$≥2，
∴$\frac{t+2}{t}$≥4，解得$t≤\frac{2}{3}$．
∴t的最大值为$\frac{2}{3}$．
故答案为：$\frac{2}{3}$．

点评 本题考查了函数的单调性、等价转化方法、数形结合思想方法，考查了推理能力与计算能力，属于难题．