
分析 (Ⅰ)由tanα=$\frac{1}{2}$求得tan2α及sinα、cosα的值,代入原函数可得函数解析式;
(Ⅱ)由an+1=f(an)求得数列递推式,把数列递推式变形,可得$\frac{1}{1+{a}_{n}}=\frac{1}{{a}_{n}}-\frac{1}{{a}_{n+1}}$,结合已知放缩得答案.
解答 (Ⅰ)解:∵tanα=$\frac{1}{2}$,α∈(0,$\frac{π}{2}}$),
∴tan2α=$\frac{2tanα}{1-ta{n}^{2}α}=\frac{2×\frac{1}{2}}{1-(\frac{1}{2})^{2}}=\frac{4}{3}$,
由$\left\{\begin{array}{l}{tanα=\frac{sinα}{cosα}=\frac{1}{2}}\\{si{n}^{2}α+co{s}^{2}α=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{sinα=\frac{\sqrt{5}}{5}}\\{cosα=\frac{2\sqrt{5}}{5}}\end{array}\right.$(0$<α<\frac{π}{2}$).
∴cos(α+$\frac{π}{4}$)=cosαcos$\frac{π}{4}$-sinαsin$\frac{π}{4}$=$\frac{2\sqrt{5}}{5}×\frac{\sqrt{2}}{2}-\frac{\sqrt{5}}{5}×\frac{\sqrt{2}}{2}=\frac{\sqrt{10}}{10}$,
∴f(x)=$\frac{3}{4}$x2tan2α+$\sqrt{10}$xcos(α+$\frac{π}{4}$)=$\frac{3}{4}×\frac{4}{3}{x}^{2}+\sqrt{10}×\frac{\sqrt{10}}{10}x={x}^{2}+x$;
(Ⅱ)证明:由an+1=f(an),得${a}_{n+1}={{a}_{n}}^{2}+{a}_{n}$,
∴${a}_{n+1}-{a}_{n}={{a}_{n}}^{2}>0$,则an+1>an≥a1,
∵an+1=an(an+1),则$\frac{1}{{a}_{n+1}}=\frac{1}{{a}_{n}({a}_{n}+1)}=\frac{1}{{a}_{n}}-\frac{1}{1+{a}_{n}}$,
∴$\frac{1}{1+{a}_{n}}=\frac{1}{{a}_{n}}-\frac{1}{{a}_{n+1}}$.
又∵a1=$\frac{2}{3}$,
∴$\frac{1}{{1+{a_1}}}$+$\frac{1}{{1+{a_2}}}$+…+$\frac{1}{{1+{a_n}}}$=$\frac{1}{{a}_{1}}-\frac{1}{{a}_{2}}+\frac{1}{{a}_{2}}-\frac{1}{{a}_{3}}+…+\frac{1}{{a}_{n}}-\frac{1}{{a}_{n+1}}$=$\frac{1}{{a}_{1}}-\frac{1}{{a}_{n+1}}$=$\frac{3}{2}-\frac{1}{{a}_{n+1}}$.
∴1<$\frac{1}{{1+{a_1}}}$+$\frac{1}{{1+{a_2}}}$+…+$\frac{1}{{1+{a_n}}}$<$\frac{3}{2}$.
点评 本题考查三角函数中的恒等变换应用,着重考查数列不等式的证明,把已知递推式灵活变形是关键,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,将平面直角坐标系中的格点(横、纵坐标均为整点的点)按如下规则标上数字标签:点(0,0)处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,点(-1,1)处标6,点(0,1)处标7,依此类推,则标签20172的格点坐标 为(1009,1008).
如图,将平面直角坐标系中的格点(横、纵坐标均为整点的点)按如下规则标上数字标签:点(0,0)处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,点(-1,1)处标6,点(0,1)处标7,依此类推,则标签20172的格点坐标 为(1009,1008).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
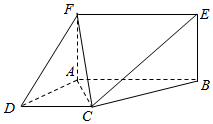 如图,已知四边形ABEF为矩形,四边形ABCD为直角梯形,平面ABEF⊥平面ABCD,∠BAD=90°,AB∥CD,AF=BC=2,CD=3,AB=4.
如图,已知四边形ABEF为矩形,四边形ABCD为直角梯形,平面ABEF⊥平面ABCD,∠BAD=90°,AB∥CD,AF=BC=2,CD=3,AB=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | K2的值可以为负值 | |
| B. | K2独立性检验的统计假设是各事件之间相互独立 | |
| C. | K2独立性检验显示“患慢性气管炎和吸烟习惯有关”即指“有吸烟习惯的人必会患慢性气管炎” | |
| D. | 2×2列联表中的4个数据可为任何实数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com