
分析 (Ⅰ)去掉绝对值符号,利用条件求m的值;
(Ⅱ)若实数a,b满足a+b=m,利用基本不等式求a2+b2的最小值.
解答 解:(Ⅰ)∵|2x-m|≤x+1
∴-x-1≤2x-m≤x+1,
∴$\frac{1}{3}$(m-1)≤x≤m+1,
∵不等式|2x-m|≤x+1的解集为[1,5].
∴$\left\{{\begin{array}{l}{m-1=3}\\{m+1=5}\end{array}⇒m=4}\right.$,
(Ⅱ)${a^2}+{b^2}≥\frac{{{{(a+b)}^2}}}{2}≥\frac{16}{2}$=8
当且仅当a=b时,取等号,
∴a2+b2的最小值为8.
点评 本题考查绝对值不等式的解法,考查基本不等式的运用,属于中档题.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知四边形ACED和四边形CBFE都是矩形,且二面角A-CE-B是直二面角,AM垂直CD交CE于M.
已知四边形ACED和四边形CBFE都是矩形,且二面角A-CE-B是直二面角,AM垂直CD交CE于M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(3\sqrt{2},\frac{3π}{4})$ | B. | $(-3\sqrt{2},\frac{5π}{4})$ | C. | $(3,\frac{5π}{4})$ | D. | $(-3,\frac{3π}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,ABC-A1B1C1是底面边长为2,高为$\frac{{\sqrt{3}}}{2}$的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).
如图,ABC-A1B1C1是底面边长为2,高为$\frac{{\sqrt{3}}}{2}$的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
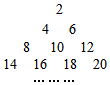 将正偶数排列如表,其中第i行第j个数表示aij(i∈N*,j∈N*),例如a32=10,若aij=2012,则i+j=( )
将正偶数排列如表,其中第i行第j个数表示aij(i∈N*,j∈N*),例如a32=10,若aij=2012,则i+j=( )| A. | 60 | B. | 61 | C. | 62 | D. | 63 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com