
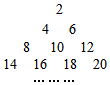 将正偶数排列如表,其中第i行第j个数表示aij(i∈N*,j∈N*),例如a32=10,若aij=2012,则i+j=( )
将正偶数排列如表,其中第i行第j个数表示aij(i∈N*,j∈N*),例如a32=10,若aij=2012,则i+j=( )| A. | 60 | B. | 61 | C. | 62 | D. | 63 |
分析 根据题目中给出的图形,归纳总结出各行各列数的个数,分析出各偶数的关系,进而可求出aij=2012时,i,j的值,进而得到答案.
解答 解:由图形可知:
第1行1个偶数,
第2行2个偶数,
…
第n行n个偶数;
∵2012是第1006个偶数,设它在第n行,则之前已经出现了n-1行,共1+2+…+(n-1)=个偶数,
∴$\frac{n(n-1)}{2}$≤1006,
解得n<45,
∴2012在第45行,
∵前44行有990个偶数,
∴2012在第45行,第16列,即i=45,j=16,
∴i+j=61,
故选:B.
点评 本题集数列和图形计数于一体,题目设计新颖,既考查了数列的知识,又考查了归纳推理的过程,是高考考查的重点内容.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
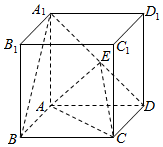 如图,在底面是菱形的四棱柱ABCD-A1B1C1D1中,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在A1D上.
如图,在底面是菱形的四棱柱ABCD-A1B1C1D1中,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在A1D上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
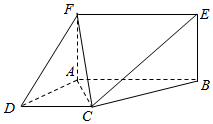 如图,已知四边形ABEF为矩形,四边形ABCD为直角梯形,平面ABEF⊥平面ABCD,∠BAD=90°,AB∥CD,AF=BC=2,CD=3,AB=4.
如图,已知四边形ABEF为矩形,四边形ABCD为直角梯形,平面ABEF⊥平面ABCD,∠BAD=90°,AB∥CD,AF=BC=2,CD=3,AB=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com