
分析 (Ⅰ)利用待定系数法求圆E的方程;
(Ⅱ)线段MN为圆F、圆E的公共弦,求出其方程,即可证明:直线MN恒过一个定点.
解答 (Ⅰ)解;设圆E的方程为(x-a)2+(y-b)2=r2,由已知得:$\left\{\begin{array}{l}{a+b-2=0}\\{(1-a)^{2}+(-1-b)^{2}={r}^{2}}\\{(-1-a)^{2}+(1-b)^{2}={r}^{2}}\end{array}\right.$
解得a=b=1,r=2 …(4分)
∴圆E的方程为(x-1)2+(y-1)2=4 …(5分)
(Ⅱ)证明:直线l关于原点对称的直线l′的方程为x+y+2=0…(7分)
由已知得,∠PME=90°=∠PNE
所以以PE为直径的圆F过点M,N,故线段MN为圆F、圆E的公共弦.…(8分)
设P(a,b),则圆F的方程为$(x-\frac{a+1}{2})^{2}+(y-\frac{b+1}{2})^{2}$=$(\frac{a+1}{2}-1)^{2}$+$(\frac{b+1}{2}-1)^{2}$
即x2+y2-(a+1)x-(b+1)y+a+b=0 ①…(9分)
又圆E的方程为x2+y2-2x-2y-2=0 ②
②-①得直线MN的方程为(a-1)x+(b-1)y-a-b-2=0…(10分)
又点P在直线l≤上,所以a+b+2=0,
∴(a-1)x+(-a-3)y=0…(11分)
∴a(x-y)-x-3y=0,
∴$\left\{\begin{array}{l}{x-y=0}\\{-x-3y=0}\end{array}\right.$,
∴x=y=0
∴直线MN过定点(0,0).…(12分)
点评 本题考查圆的方程,考查直线与圆、圆与圆的位置关系,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
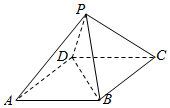 在四棱锥P-ABCD中,底面ABCD是菱形,AB=2,∠BAD=60°,PC⊥BD.
在四棱锥P-ABCD中,底面ABCD是菱形,AB=2,∠BAD=60°,PC⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4949 | B. | 4950 | C. | 4951 | D. | 4952 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知四边形ACED和四边形CBFE都是矩形,且二面角A-CE-B是直二面角,AM垂直CD交CE于M.
已知四边形ACED和四边形CBFE都是矩形,且二面角A-CE-B是直二面角,AM垂直CD交CE于M.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
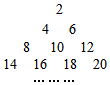 将正偶数排列如表,其中第i行第j个数表示aij(i∈N*,j∈N*),例如a32=10,若aij=2012,则i+j=( )
将正偶数排列如表,其中第i行第j个数表示aij(i∈N*,j∈N*),例如a32=10,若aij=2012,则i+j=( )| A. | 60 | B. | 61 | C. | 62 | D. | 63 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com