
分析 过N作l的垂线,垂足为Q,则|NF|=|NQ|,|PF|=|PM|,于是∠PFM=∠PMF=∠MFO=∠MNQ,$\frac{|MN|}{|NF|}$=$\sqrt{5}$,则cos∠MNQ,利用二倍角公式求出tan∠MFO,然后求出P的坐标,即可得到直线的斜率.
解答 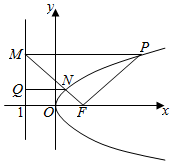 解:抛物线C:y2=4x的焦点为F(1,0),
解:抛物线C:y2=4x的焦点为F(1,0),
过N作l的垂线,垂足为Q,则|NF|=|NQ|,
$\frac{|MN|}{|NF|}$=$\sqrt{5}$,则$\frac{|MN|}{|QN|}$=$\sqrt{5}$,∴cos∠MNQ=$\frac{\sqrt{5}}{5}$.
∴cos∠MFO=$\frac{\sqrt{5}}{5}$.tan∠MFO=2,
∴M(-1,4),∴P(4,4).
∴${K}_{PF}=\frac{4-0}{4-1}$=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查了抛物线的性质,三角函数的恒等变换,属于中档题.


科目:高中数学 来源: 题型:选择题
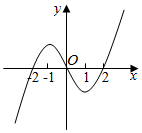 已知R上的可导函数f(x)的图象如图所示,两个极值点分别为-1和1,若f′(x)为函数f(x)的导函数,则不等式(x2-2x-3)f′(x)>0的解集为( )
已知R上的可导函数f(x)的图象如图所示,两个极值点分别为-1和1,若f′(x)为函数f(x)的导函数,则不等式(x2-2x-3)f′(x)>0的解集为( )| A. | (-∞,-2)∪(1,+∞) | B. | (-∞,-1)∪(-1,1)∪(3,+∞) | C. | (-∞,-1)∪(-1,0)∪(2,+∞) | D. | (-∞,-2)∪(1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com