
分析 (1)当m=1时,不等式f(x)<2可化为x+|x-1|<2,分类讨论,去掉绝对值符合,即可求不等式f(x)<2的解集;
(2)方程f(x)=$\frac{1}{3}$可转化为|mx-1|=$\frac{1}{3}$-x,利用方程f(x)=$\frac{1}{3}$有两个不同的实数根,得出-m<-1且$\frac{1}{m}$<$\frac{1}{3}$,即可求出实数m的取值范围.
解答  解:(1)当m=1时,不等式f(x)<2可化为x+|x-1|<2,
解:(1)当m=1时,不等式f(x)<2可化为x+|x-1|<2,
x≤1时,原不等式可化为:x-x+1<2,恒成立;
x>1时,原不等式可化为:x+x-1<2,解得:x<1.5,
∴1<x<1.5.
综上所述,x<1.5,
∴不等式f(x)<2的解集为{x|x<1.5};
(2)方程f(x)=$\frac{1}{3}$可转化为|mx-1|=$\frac{1}{3}$-x,mx-1=0的根为$\frac{1}{m}$,y=$\frac{1}{3}$-x的斜率为-1.
∵方程f(x)=$\frac{1}{3}$有两个不同的实数根,
∴-m<-1且$\frac{1}{m}$<$\frac{1}{3}$,
∴m>3.
点评 本题考查不等式的解法,考查方程根的问题,正确转化是关键.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $(3\sqrt{2},\frac{3π}{4})$ | B. | $(-3\sqrt{2},\frac{5π}{4})$ | C. | $(3,\frac{5π}{4})$ | D. | $(-3,\frac{3π}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
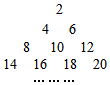 将正偶数排列如表,其中第i行第j个数表示aij(i∈N*,j∈N*),例如a32=10,若aij=2012,则i+j=( )
将正偶数排列如表,其中第i行第j个数表示aij(i∈N*,j∈N*),例如a32=10,若aij=2012,则i+j=( )| A. | 60 | B. | 61 | C. | 62 | D. | 63 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{5}{110}$ | C. | $\frac{1}{20}$ | D. | $\frac{5}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com