
分析 (1)半圆C的极坐标方程为ρ=4sinθ($\frac{π}{4}$<θ<$\frac{3π}{4}$),即ρ2=4ρsinθ,利用互化公式可得直角坐标方程,注意y的取值范围.直线l:$\left\{\begin{array}{l}x=a+\sqrt{2}t\\ y=a+\frac{{\sqrt{2}}}{2}t\end{array}$(t为参数),消去参数t化为普通方程.
(2)如图所示,直线l经过点(-2,2)时,即a=6时,直线与圆有两个交点.当直线与半圆相切时,$\frac{|-4+a|}{\sqrt{5}}$=2,解得a,结合图形即可得出.
解答 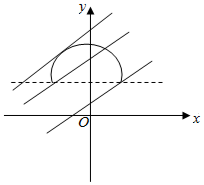 解:(1)半圆C的极坐标方程为ρ=4sinθ($\frac{π}{4}$<θ<$\frac{3π}{4}$),
解:(1)半圆C的极坐标方程为ρ=4sinθ($\frac{π}{4}$<θ<$\frac{3π}{4}$),
即ρ2=4ρsinθ,化为x2+y2=4y,平方为x2+(y-2)2=4(2≤y≤4).
直线l:$\left\{\begin{array}{l}x=a+\sqrt{2}t\\ y=a+\frac{{\sqrt{2}}}{2}t\end{array}$(t为参数),消去参数t化为普通方程:x-2y+a=0.
(2)如图所示,直线l经过点(-2,2)时,即-2-2×2+a=0,
解得a=6时,直线与圆有两个交点.
当直线与半圆相切时,$\frac{|-4+a|}{\sqrt{5}}$=2,解得a=4$±2\sqrt{5}$,取a=4+2$\sqrt{5}$.
∴当$6≤a<4+2\sqrt{5}$时,直线l与曲线C有且只有2个公共点.
∴实数a的取值范围是$[6,4+2\sqrt{5})$.
点评 本题考查了极坐标化为直角坐标、参数方程化为普通方程、直线与圆相交相切问题、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,将平面直角坐标系中的格点(横、纵坐标均为整点的点)按如下规则标上数字标签:点(0,0)处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,点(-1,1)处标6,点(0,1)处标7,依此类推,则标签20172的格点坐标 为(1009,1008).
如图,将平面直角坐标系中的格点(横、纵坐标均为整点的点)按如下规则标上数字标签:点(0,0)处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,点(-1,1)处标6,点(0,1)处标7,依此类推,则标签20172的格点坐标 为(1009,1008).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
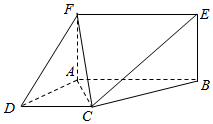 如图,已知四边形ABEF为矩形,四边形ABCD为直角梯形,平面ABEF⊥平面ABCD,∠BAD=90°,AB∥CD,AF=BC=2,CD=3,AB=4.
如图,已知四边形ABEF为矩形,四边形ABCD为直角梯形,平面ABEF⊥平面ABCD,∠BAD=90°,AB∥CD,AF=BC=2,CD=3,AB=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com