
分析 运用作差比较法,将2(a4+b4)-ab(a+b)2,展开分组,运用提取公因式和完全平方公式,以及立方差和平方差公式,因式分解,判断符号,即可得证.
解答 证明:2(a4+b4)-ab(a+b)2=2(a4+b4)-ab(a2+2ab+b2)
=(a4+b4-a3b-ab3)+(a4-2a2b2+b4)
=[a3(a-b)-b3(a-b)]+(a2-b2)2
=(a-b)(a3-b3)+(a-b)2(a+b)2,
=(a-b)2(a2+ab+b2+a2+2ab+b2)
=(a-b)2(2a2+3ab+2b2),
由(a-b)2≥0,2a2+3ab+2b2=2(a+$\frac{3}{4}$b)2+$\frac{7}{8}$b2≥0,
可得(a-b)2(2a2+3ab+2b2)≥0,
则a4+b4≥$\frac{1}{2}$ab(a+b)2.
点评 本题考查不等式的证明,注意运用作差比较法,以及分解因式的方法,运用平方非负数和配方判断符号,属于中档题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
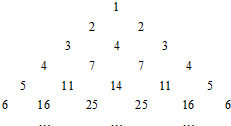 如图的三角形数阵中,满足:
如图的三角形数阵中,满足:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,0) | B. | (π,-π) | C. | (2,$\frac{π}{4}$) | D. | (π,-$\frac{3π}{4}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com