
分析 (1)曲线C的参数方程为$\left\{\begin{array}{l}{x=t+\frac{1}{t}}\\{y=t-\frac{1}{t}}\end{array}\right.$(t为参数),平方相减可得:x2-y2=4.直线l的极坐标方程为ρsin($θ-\frac{π}{3}$)=2,展开化为:$\frac{1}{2}ρsinθ$-$\frac{\sqrt{3}}{2}ρcosθ$=2,利用互化公式可得直角坐标方程:$\sqrt{3}$x-y+4=0.
(2)设与直线l平行的直线1′的方程为:$\sqrt{3}$x-y+m=0,把点E(3,0)代入解得m.可得直线1′的方程,与x2-y2=4联立化为:2x2-18x+23=0.利用根与系数的关系可得|AB|=$\sqrt{(1+3)[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$.
解答 解:(1)曲线C的参数方程为$\left\{\begin{array}{l}{x=t+\frac{1}{t}}\\{y=t-\frac{1}{t}}\end{array}\right.$(t为参数),
则x2-y2=$(t+\frac{1}{t})^{2}$-$(t-\frac{1}{t})^{2}$$\frac{2}{t}×2t$=4.可得直角坐标方程:x2-y2=4.
直线l的极坐标方程为ρsin($θ-\frac{π}{3}$)=2,
展开化为:$\frac{1}{2}ρsinθ$-$\frac{\sqrt{3}}{2}ρcosθ$=2,可得直角坐标方程:$\sqrt{3}$x-y+4=0.
(2)设与直线l平行的直线1′的方程为:$\sqrt{3}$x-y+m=0,把点E(3,0)代入可得:$3\sqrt{3}$+m=0,解得m=-3$\sqrt{3}$.
∴直线1′的方程为:$\sqrt{3}$x-y-3$\sqrt{3}$=0,与x2-y2=4联立化为:2x2-18x+23=0.
∴x1+x2=9,x1x2=$\frac{23}{2}$.
∴|AB|=$\sqrt{(1+3)[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=2$\sqrt{{9}^{2}-4×\frac{23}{2}}$=2$\sqrt{35}$.
点评 本题考查了极坐标与直角坐标方程的互化、参数方程化为普通方程及其应用、直线与双曲线相交弦长、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | K2的值可以为负值 | |
| B. | K2独立性检验的统计假设是各事件之间相互独立 | |
| C. | K2独立性检验显示“患慢性气管炎和吸烟习惯有关”即指“有吸烟习惯的人必会患慢性气管炎” | |
| D. | 2×2列联表中的4个数据可为任何实数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (-∞,2] | C. | [-2,+∞) | D. | (-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
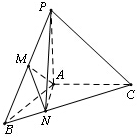 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP=1,M为PB的中点,N在BC上,且BN=$\frac{1}{3}$BC.
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP=1,M为PB的中点,N在BC上,且BN=$\frac{1}{3}$BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
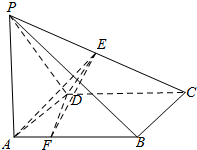 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PCD⊥底面ABCD,PD=DC=2,∠PDC=120°,E是线段PC的中点,$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AB}$.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PCD⊥底面ABCD,PD=DC=2,∠PDC=120°,E是线段PC的中点,$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AB}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com