
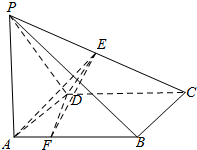
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PCD⊥底面ABCD,PD=DC=2,∠PDC=120°,E是线段PC的中点,$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AB}$.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PCD⊥底面ABCD,PD=DC=2,∠PDC=120°,E是线段PC的中点,$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AB}$.分析 (Ⅰ)证明:DC⊥面EFH,即可证明:EF⊥CD;
(Ⅱ)根据点F到平面ADE的距离等于点H到平面ADE的距离,即可求点F到平面ADE的距离.
解答 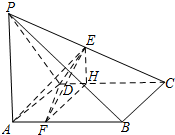
 证明:(Ⅰ)在侧面PCD中,PD=DC=2,∠PDC=120°,E是PC中点,
证明:(Ⅰ)在侧面PCD中,PD=DC=2,∠PDC=120°,E是PC中点,
∴DE=1,
过E作EH⊥DC于H,连结FH,
∵底面ABCD是正方形,$\overrightarrow{AF}=\frac{1}{4}\overrightarrow{AB}$,
即$AF=\frac{1}{2}$,
∴AFHD是矩形,
∴FH⊥DC,…(3分)
又EH⊥DC,EH∩FH=H,
∴DC⊥面EFH,…(5分)
又∵EF?面EFH,
∴DC⊥EF. …(6分)
解:(II)由(I)知,FH∥平面ADE,
∴点F到平面ADE的距离等于点H到平面ADE的距离,…(7分)
∵底面ABCD是正方形,侧面PCD⊥底面ABCD,
∴AD⊥侧面PDC,
即AD⊥侧面DEH,
∴AD⊥DE,
${V_{A-DEH}}=\frac{1}{3}•{S_{DEH}}•AD$,
在三棱锥H-ADE中,设点H到平面ADE的距离为d,则${V_{H-ADE}}=\frac{1}{3}•{S_{ADE}}•d$,…(9分)
由于VH-ADE=VA-DEH,
∴$\frac{1}{3}•{S_{DEH}}•AD$=$\frac{1}{3}•{S_{ADE}}•d$,
∴DH•EH•AD=AD•DE•d,
∴$\frac{1}{2}•\frac{{\sqrt{3}}}{2}•2$=2•1•d,…(11分)
∴$d=\frac{{\sqrt{3}}}{4}$,
即点F到平面ADE的距离为$\frac{{\sqrt{3}}}{4}$. …(12分)
点评 本题考查线面垂直的证明,考查点到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
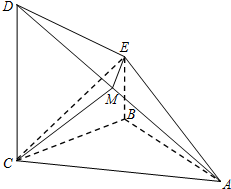 如图,四棱锥A-BCDE中,CD⊥平面ABC,BE∥CD,AB=BC=CD,AB⊥BC,M为AD上一点,EM⊥平面ACD.
如图,四棱锥A-BCDE中,CD⊥平面ABC,BE∥CD,AB=BC=CD,AB⊥BC,M为AD上一点,EM⊥平面ACD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{15}{2}$ | B. | $\frac{40}{3}$ | C. | $\frac{18}{5}$ | D. | $\frac{24}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,0) | B. | (π,-π) | C. | (2,$\frac{π}{4}$) | D. | (π,-$\frac{3π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱柱ABC-A1B1C1为正三棱柱,BC=CC1=4,D是A1C1中点.
如图,三棱柱ABC-A1B1C1为正三棱柱,BC=CC1=4,D是A1C1中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M和N | B. | M和G | C. | M和H | D. | N和H |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com