
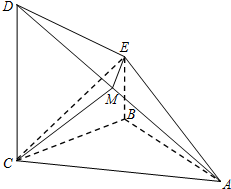
 如图,四棱锥A-BCDE中,CD⊥平面ABC,BE∥CD,AB=BC=CD,AB⊥BC,M为AD上一点,EM⊥平面ACD.
如图,四棱锥A-BCDE中,CD⊥平面ABC,BE∥CD,AB=BC=CD,AB⊥BC,M为AD上一点,EM⊥平面ACD.分析 (Ⅰ)取AC的中点F,连接BF,证明BF⊥平面ACD,结合EM⊥平面ACD,所以EM∥BF,再结合线面平行的判定定理得到EM∥面ABC;
(Ⅱ)由等面积法求出点D到平面EMC的距离.
解答  证明:(Ⅰ)取AC的中点F,连接BF,
证明:(Ⅰ)取AC的中点F,连接BF,
因为AB=BC,所以BF⊥AC,
又因为CD⊥平面ABC,所以CD⊥BF,
所以BF⊥平面ACD,…(3分)
因为EM⊥平面ACD,
所以EM∥BF,
因为EM?面ABC,BF?平面ABC,
所以EM∥平面ABC; …(6分)
解:(Ⅱ)因为EM⊥平面ACD,EM?面EMC,
所以平面CME⊥平面ACD,平面CME∩平面ACD=CM,
过点D作直线DG⊥CM,则DG⊥平面CME,…(9分)
由已知CD⊥平面ABC,BE∥CD,AB=BC=CD=2BE,可得AE=DE,
又EM⊥AD,
所以M为AD的中点,
在Rt△ABC中,$AC=\sqrt{2}BC=2\sqrt{2}$,
在Rt△ADC中,$AD=\sqrt{C{D^2}+A{C^2}}=2\sqrt{3}$,
${S_{△CDM}}=\frac{1}{2}{S_{△ACD}}=\frac{1}{2}×\frac{1}{2}×2×2\sqrt{2}=\sqrt{2}$,
在△DCM中,$CM=\frac{1}{2}AD=\sqrt{3}$,
由等面积法知$\frac{1}{2}×CM×DG=\sqrt{2}$,
所以$DG=\frac{{2\sqrt{6}}}{3}$,
即点D到平面EMC的距离为$\frac{{2\sqrt{6}}}{3}$.…(12分)
点评 本题考查的知识点是直线与平面平行的判定,点D到平面EMC的距离,其中熟练掌握空间线面平行或垂直的判定、性质、定义、几何特征是解答此类问题的关键.


科目:高中数学 来源: 题型:选择题
| A. | K2的值可以为负值 | |
| B. | K2独立性检验的统计假设是各事件之间相互独立 | |
| C. | K2独立性检验显示“患慢性气管炎和吸烟习惯有关”即指“有吸烟习惯的人必会患慢性气管炎” | |
| D. | 2×2列联表中的4个数据可为任何实数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
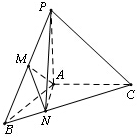 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP=1,M为PB的中点,N在BC上,且BN=$\frac{1}{3}$BC.
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP=1,M为PB的中点,N在BC上,且BN=$\frac{1}{3}$BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 收看 | 不收看 | 总计 | |
| 45岁以上 | |||
| 45岁以下 | |||
| 总计 |
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| K0 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
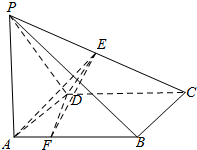 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PCD⊥底面ABCD,PD=DC=2,∠PDC=120°,E是线段PC的中点,$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AB}$.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PCD⊥底面ABCD,PD=DC=2,∠PDC=120°,E是线段PC的中点,$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AB}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,正方形BCDE的边长为a,已知AB=$\sqrt{3}$BC,将直角△ABE沿BE边折起,A点在平面BCDE上的射影为D点,则对翻折后的几何体有如下描述:
如图,正方形BCDE的边长为a,已知AB=$\sqrt{3}$BC,将直角△ABE沿BE边折起,A点在平面BCDE上的射影为D点,则对翻折后的几何体有如下描述:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com