
 如图,正方形BCDE的边长为a,已知AB=$\sqrt{3}$BC,将直角△ABE沿BE边折起,A点在平面BCDE上的射影为D点,则对翻折后的几何体有如下描述:
如图,正方形BCDE的边长为a,已知AB=$\sqrt{3}$BC,将直角△ABE沿BE边折起,A点在平面BCDE上的射影为D点,则对翻折后的几何体有如下描述:分析 对于①,由于BC∥DE,则∠ABC(或其补角)为AB与DE所成角,求出tan∠ABC加以判断;
对于②,根据三棱锥的体积公式即可求VB-ACE的体积;
对于③,确定∠BAE为直线BA与平面ADE所成角,求解即可判断;
对于④,证明BE⊥平面ADE,利用面面平行的判定,可得平面EAB⊥平面ADE;
对于⑤,把四棱锥A-BCDE的外接球,转化为以D为一个顶点,以DA、DC、DE为三条棱的正方体的外接球求解判断.
解答 解:作出折叠后的几何体直观图如图所示:
对于①,∵AB=$\sqrt{3}$a,BE=a,∴AE=$\sqrt{2}$a.
∴AD=$\sqrt{A{E}^{2}-D{E}^{2}}=a$,∴AC=$\sqrt{C{D}^{2}+A{D}^{2}}=\sqrt{2}a$.
在△ABC中,cos∠ABC=$\frac{A{B}^{2}+B{C}^{2}-A{C}^{2}}{2AB•BC}=\frac{3{a}^{2}+{a}^{2}-2{a}^{2}}{2\sqrt{3}{a}^{2}}$=$\frac{\sqrt{3}}{3}$,
∴sin∠ABC=$\sqrt{1-co{s}^{2}∠ABC}=\frac{\sqrt{6}}{3}$,
∴tan∠ABC=$\frac{sin∠ABC}{cos∠ABC}=\sqrt{2}$.
∵BC∥DE,∴∠ABC是异面直线AB,DE所成的角,故①正确;
对于②,三棱锥B-ACE的体积V=$\frac{1}{3}{S}_{△BCE}•AD=\frac{1}{3}×\frac{1}{2}{a}^{2}•a=\frac{1}{6}{a}^{3}$,故②正确;
对于③,∵BE⊥平面ADE,∴∠BAE为直线BA与平面ADE所成角,
在△BAE中,∠BEA=90°,BE=a,AB=$\sqrt{3}$a,
∴sin∠BEA=$\frac{BE}{AB}=\frac{a}{\sqrt{3}a}=\frac{\sqrt{3}}{3}$,故③错误;
对于④,∵AD⊥平面BCDE,BE?平面BCDE,∴AD⊥BE,
∵BE⊥ED,AD∩ED=D,∴BE⊥平面ADE,
∵BE?平面EAB,∴平面EAB⊥平面ADE,故④正确;
对于⑤,四棱锥A-BCDE的外接球,即以D为一个顶点,以DA、DC、DE为三条棱的正方体的外接球,其半径R满足(2R)2=3a2,
∴R=$\frac{\sqrt{3}}{2}a$,则棱锥A-BCDE的外接球的表面积为4π•$(\frac{\sqrt{3}}{2}a)^{2}=3π{a}^{2}$,故⑤错误.
∴错误的命题是③⑤.
故答案为:③⑤.
点评 本题考查图形的翻折,考查空间线面位置关系,搞清翻折前后的变与不变是关键,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
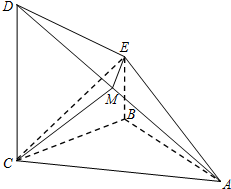 如图,四棱锥A-BCDE中,CD⊥平面ABC,BE∥CD,AB=BC=CD,AB⊥BC,M为AD上一点,EM⊥平面ACD.
如图,四棱锥A-BCDE中,CD⊥平面ABC,BE∥CD,AB=BC=CD,AB⊥BC,M为AD上一点,EM⊥平面ACD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M和N | B. | M和G | C. | M和H | D. | N和H |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线的一部分 | B. | 圆的一部分 | C. | 椭圆的一部分 | D. | 抛物线的一部分 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com