
分析 可判断f(x)<0恒成立;从而化简方程为f(x)=-lnm,从而作图辅助,可知存在实数a(a≤-1),使-2x1=a=-${e}^{-{x}_{2}}$,从而可得x1+x2=-$\frac{a}{2}$-ln(-a),再构造函数,求导,从而确定最值.
解答 解:∵f(x)=$\left\{\begin{array}{l}{-2x,(x>0)}\\{-{e}^{-x}(x≤0)}\end{array}\right.$,∴f(x)<0恒成立;
∴f[f(x)]=-e-f(x),
∵f[f(x)]+m=0,
∴-e-f(x)+m=0,即f(x)=-lnm;
作函数f(x)=$\left\{\begin{array}{l}{-2x,(x>0)}\\{-{e}^{-x}(x≤0)}\end{array}\right.$,y=-lnm的图象如下,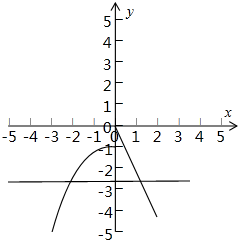 ,
,
结合图象可知,存在实数a(a≤-1),使-2x1=a=-${e}^{-{x}_{2}}$,
故x1+x2=-$\frac{a}{2}$-ln(-a),
令g(a)=-$\frac{a}{2}$-ln(-a),则g′(a)=-$\frac{2+a}{2a}$,
故当a=-2时,x1+x2有最大值1-ln2;
故答案为:1-ln2.
点评 本题考查了复合函数与分段函数的应用,同时考查了导数的综合应用及最值问题,应用了数形结合的思想及转化构造的方法.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:填空题
 如图,正方形BCDE的边长为a,已知AB=$\sqrt{3}$BC,将直角△ABE沿BE边折起,A点在平面BCDE上的射影为D点,则对翻折后的几何体有如下描述:
如图,正方形BCDE的边长为a,已知AB=$\sqrt{3}$BC,将直角△ABE沿BE边折起,A点在平面BCDE上的射影为D点,则对翻折后的几何体有如下描述:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
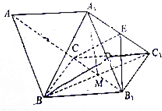 如图,在三棱柱ABC-A1B1C1中,点A1在侧面BB1C1C上的射影为正方形BB1C1C的中心M,且BB1=2$\sqrt{2}$,AB=AC=3,E为A1C1的中点.
如图,在三棱柱ABC-A1B1C1中,点A1在侧面BB1C1C上的射影为正方形BB1C1C的中心M,且BB1=2$\sqrt{2}$,AB=AC=3,E为A1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
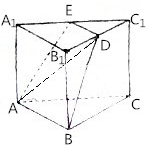 如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=2,AA1=$\sqrt{2}$,E是A1C1边的中点,过A,B,E作截面交B1C1于点D
如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=2,AA1=$\sqrt{2}$,E是A1C1边的中点,过A,B,E作截面交B1C1于点D查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0) | D. | (-∞,-2)∪(0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
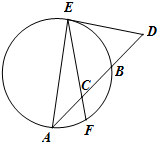 如图,设D是弦AB延长线上一点,且AB=2BD,过D作圆的切线于E,若C为线段AB的中点,连结EC交圆于点F,若$BC=\sqrt{3}CF$.
如图,设D是弦AB延长线上一点,且AB=2BD,过D作圆的切线于E,若C为线段AB的中点,连结EC交圆于点F,若$BC=\sqrt{3}CF$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com