
分析 (1)点A(2,$\frac{π}{3}$)关于极轴的对称点为B(2,-$\frac{π}{3}$),直线AB的直角坐标方程为:x=2cos$\frac{π}{3}$,化简可得极坐标方程.
(2)设△AOB的外接圆的圆心O′(x,0),则x=$\sqrt{(\sqrt{3})^{2}+(x-1)^{2}}$,化简可得直角坐标方程,进而得到△AOB外接圆的极坐标方程.
解答 解:(1)点A(2,$\frac{π}{3}$)关于极轴的对称点为B(2,-$\frac{π}{3}$),
直线AB的直角坐标方程为:x=2cos$\frac{π}{3}$=1,可得极坐标方程:ρcosθ=1.
(2)设△AOB的外接圆的圆心O′(x,0),则x=$\sqrt{(\sqrt{3})^{2}+(x-1)^{2}}$,化为:x=2.
∴△AOB外接圆的极坐标方程为ρcosθ=2.
点评 本题考查了极坐标与直角坐标方程的互化、直线与圆相交弦长、勾股定理、直角三角形的边角关系,考查了推理能力与计算能力,属于中档题.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,将平面直角坐标系中的格点(横、纵坐标均为整点的点)按如下规则标上数字标签:点(0,0)处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,点(-1,1)处标6,点(0,1)处标7,依此类推,则标签20172的格点坐标 为(1009,1008).
如图,将平面直角坐标系中的格点(横、纵坐标均为整点的点)按如下规则标上数字标签:点(0,0)处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,点(-1,1)处标6,点(0,1)处标7,依此类推,则标签20172的格点坐标 为(1009,1008).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
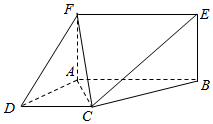 如图,已知四边形ABEF为矩形,四边形ABCD为直角梯形,平面ABEF⊥平面ABCD,∠BAD=90°,AB∥CD,AF=BC=2,CD=3,AB=4.
如图,已知四边形ABEF为矩形,四边形ABCD为直角梯形,平面ABEF⊥平面ABCD,∠BAD=90°,AB∥CD,AF=BC=2,CD=3,AB=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | K2的值可以为负值 | |
| B. | K2独立性检验的统计假设是各事件之间相互独立 | |
| C. | K2独立性检验显示“患慢性气管炎和吸烟习惯有关”即指“有吸烟习惯的人必会患慢性气管炎” | |
| D. | 2×2列联表中的4个数据可为任何实数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 收看 | 不收看 | 总计 | |
| 45岁以上 | |||
| 45岁以下 | |||
| 总计 |
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| K0 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com