
分析 (Ⅰ)当m=1时,把要解不等式f(x)+f(2x)>1等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
(Ⅱ)证明:当x≥1时,利用绝对值三角不等式求得f(x)+f(-$\frac{1}{2x}}$)≥x+$\frac{1}{2x}$,再根据h(x)=x+$\frac{1}{2x}$ 在[1,+∞)上单调递增,可得h(x)≥h(1),从而证得不等式成立.
解答 解:(Ⅰ)当m=1时,不等式f(x)+f(2x)>1,即|x-m|+|2x-2m|>1.
令m(x)=|x-m|+|2x-2m|=$\left\{\begin{array}{l}{-3x+2,x<\frac{1}{2}}\\{x,\frac{1}{2}≤x<1}\\{3x-2,x≥1}\end{array}\right.$,则不等式即$\left\{\begin{array}{l}{-3x+2>1}\\{x<\frac{1}{2}}\end{array}\right.$ ①,或 $\left\{\begin{array}{l}{x>1}\\{\frac{1}{2}≤x<1}\end{array}\right.$ ②,或 $\left\{\begin{array}{l}{3x-2>1}\\{x≥1}\end{array}\right.$③.
解①求得x<$\frac{1}{3}$,解②求得 x∈∅,解③求得x>1.
综上可得,原不等式的解集为{x|x<$\frac{1}{3}$,或x>1 }.
证明:(Ⅱ)当x≥1时,f(x)+f(-$\frac{1}{2x}}$)=|x-m|+|-m-$\frac{1}{2x}$|≥|x-m+m+$\frac{1}{2x}$|=|x+$\frac{1}{2x}$|=x+$\frac{1}{2x}$.
由于h(x)=x+$\frac{1}{2x}$ 在[1,+∞)上单调递增,
∴h(x)≥h(1)=1+$\frac{1}{2}$=$\frac{3}{2}$,
∴f(x)+f(-$\frac{1}{2x}}$)≥$\frac{3}{2}$ 成立.
点评 本题主要考查带有绝对值的函数,绝对值三角不等式,属于中档题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
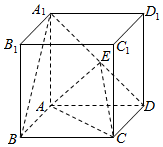 如图,在底面是菱形的四棱柱ABCD-A1B1C1D1中,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在A1D上.
如图,在底面是菱形的四棱柱ABCD-A1B1C1D1中,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在A1D上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3π | B. | 6 | C. | 12 | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,将平面直角坐标系中的格点(横、纵坐标均为整点的点)按如下规则标上数字标签:点(0,0)处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,点(-1,1)处标6,点(0,1)处标7,依此类推,则标签20172的格点坐标 为(1009,1008).
如图,将平面直角坐标系中的格点(横、纵坐标均为整点的点)按如下规则标上数字标签:点(0,0)处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,点(-1,1)处标6,点(0,1)处标7,依此类推,则标签20172的格点坐标 为(1009,1008).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com