
定义在R上的函数 ,满足当
,满足当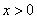 时,
时, >1,且对任意的
>1,且对任意的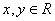 ,有
,有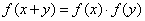 ,
,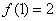 .
.
(1)求 的值;
的值;
(2)求证:对任意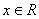 ,都有
,都有 >0;
>0;
(3)解不等式
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
某公司开发一新产品有甲、 乙两种型号,现分别对这两种型号产品进行质量检测, 从它们的检测数据中随机抽取8 次( 数值越大产品质量越好) , 记录如下:
甲:8 .3 , 9 .0 , 7 .9 , 7 .8 , 9 .4 , 8 .9 , 8 .4 , 8 .3
乙:9 .2 , 9 .5 , 8 .0 , 7 .5 , 8 .2 , 8 .1 , 9 .0 , 8 .5
(Ⅰ) 画出甲、 乙两产品数据的茎叶图;
(Ⅱ) 现要从甲、 乙中选一种型号产品投入生产, 从统计学角度, 你认为生产哪种型号产品合适?简单说明理由;
(Ⅲ) 若将频率视为概率, 对产品乙今后的三次检测数据进行预测, 记这三次数据中不低于8.5 分的次数为ξ , 求ξ的分布列及期望Eξ .
查看答案和解析>>
科目:高中数学 来源: 题型:
直线5x-2y-10=0在x轴上的截距为a,在y轴上的截距为b,则( )
A.a=2,b=5; B.a=2,b=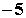 ; C.a=
; C.a=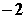 ,b=5; D.a=
,b=5; D.a=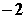 ,b=
,b=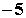 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com