练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设定义域为R的函数f(x)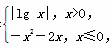＝则关于x的函数y＝2f2(x)－3f(x)＋1的零点的个数为________．


    7

    解析　由y＝2f2(x)－3f(x)＋1＝0得f(x)＝或f(x)＝1，

    如图画出f(x)的图象，由f(x)＝知有4个根，

    由f(x)＝1知有3个根，故函数y＝2f2(x)－3f(x)＋1共有7个零点．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    定义在R上的函数，满足当时，>1，且对任意的，有，.

    (1)求的值；

    (2)求证：对任意，都有>0；

    (3)解不等式

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝lg(1－x2)，集合A＝{x|y＝f(x)}，B＝{y|y＝f(x)}，则图中阴影部分表示的集合为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合A＝{1，a}，B＝{1,2,3}，则“a＝3”是“A⊆B”的________条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知命题p：“∀x∈[1,2]，x2－ln x－a≥0”是真命题，则实数a的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    方程x2－x－m＝0在x∈[－1,1]上有实根，则m的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知定义在R上的单调递增奇函数f(x)，若当0≤θ≤时，f(cos2θ＋2msin θ)＋f(－2m－2)<0恒成立，则实数m的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    为了响应国家号召，某地决定分批建设保障性住房供给社会．首批计划用100万元购得一块土地，该土地可以建造每层1 000平方米的楼房，楼房的每平方米建筑费用与建筑高度有关，楼房每升高一层，整层楼每平方米建筑费用提高20元．已知建筑第5层楼房时，每平方米建筑费用为800元．

    (1)若建筑第x层楼时，该楼房综合费用为y万元(综合费用是建筑费用与购地费用之和)，写出y＝f(x)的表达式；

    (2)为了使该楼房每平方米的平均综合费用最低，应把楼层建成几层？此时平均综合费用为每平方米多少元？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    阅读下边程序框图，为使输出的数据为，则判断框中

    应填入的条件为 （　　）                      

    （A）4

    （B）5

    （C）6

    （D）7

    查看答案和解析>>

    同步练习册答案