
已知定义在R上的单调递增奇函数f(x),若当0≤θ≤ 时,f(cos2θ+2msin θ)+f(-2m-2)<0恒成立,则实数m的取值范围是________.
时,f(cos2θ+2msin θ)+f(-2m-2)<0恒成立,则实数m的取值范围是________.
(-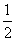 ,+∞)
,+∞)
解析 方法一 f(cos2θ+2msin θ)+f(-2m-2)<0⇒f(cos2θ+2msin θ)<f(2m+2)⇒cos2θ+2msin θ<2m+2⇒2m(1-sin θ)>-1-sin2θ.
当θ= 时,2m·0>-2,此时m∈R;
时,2m·0>-2,此时m∈R;
当0≤θ< 时,m>
时,m>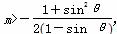 令t=1-sin θ,
令t=1-sin θ,
则t∈(0,1],此时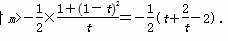 .
.
设φ(t)=-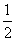 (t+
(t+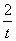 -2),
-2),
而φ(t)在t∈(0,1]上的值域是(-∞,-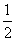 ],
],
故m>-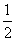 .
.
方法二 同方法一,求得2m(1-sin θ)>-1-sin2θ,
设sin θ=t,则t2-2mt+2m+1>0对于t∈[0,1]恒成立.
设g(t)=t2-2mt+2m+1,其图象的对称轴方程为t=m.
①当m<0时,g(t)在[0,1]上单调递增,
从而g(0)=2m+1>0,即m>-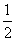 ,
,
又m<0,所以-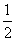 <m<0.
<m<0.
②当0≤m≤1时,g(t)在[0,m]上单调递减,在[m,1]上单调递增,
从而g(m)=m2-2m2+2m+1>0,即m2-2m-1<0,
所以1-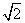 <m<1+
<m<1+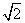 .
.
又m∈[0,1],所以0≤m≤1.
③当m>1时,g(t)在[0,1]上单调递减,
从而g(1)=1-2m+2m+1=2>0恒成立,所以m>1.
综合①②③,可知m>-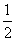 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知函数f(x)= 的定义域为集合A,函数g(x)=lg(-x2+2x+m)的定义域为集合B.
的定义域为集合A,函数g(x)=lg(-x2+2x+m)的定义域为集合B.
(1)当m=3时,求A∩(∁RB);
(2)若A∩B={x|-1<x<4},求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
若a<b<c,则函数f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)的两个零点分别位于下列哪个区间________.(填序号)
①(a,b)和(b,c)内
②(-∞,a)和(a,b)内
③(b,c)和(c,+∞)内
④(-∞,a)和(c,+∞)内
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,在直角坐标系xOy中,点P(1, )到抛物线C:y2=2px(p>0)的准线的距离为
)到抛物线C:y2=2px(p>0)的准线的距离为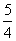 .点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB的中点Q(m,n)在直线OM上.
.点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB的中点Q(m,n)在直线OM上.

(1)求曲线C的方程及t的值;
(2)记d= ,求d的最大值.
,求d的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com