
【题目】对于函数![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 的“不动点”;若
的“不动点”;若![]() ,则称
,则称![]() 为
为![]() 的“稳定点”.函数
的“稳定点”.函数![]() 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为![]() 和
和![]() ,即
,即![]() ,
,![]() .
.
(![]() )设函数
)设函数![]() ,求集合
,求集合![]() 和
和![]() .
.
(![]() )求证:
)求证:![]() .
.
(![]() )设函数
)设函数![]() ,且
,且![]() ,求证:
,求证:![]() .
.
【答案】(![]() )
)![]() ,
,![]() .
.
(![]() )证明见解析.
)证明见解析.
(![]() )证明见解析.
)证明见解析.
【解析】
(![]() )根据函数定义,求得不动点的表达式,根据方程即可求得集合A和集合B。
)根据函数定义,求得不动点的表达式,根据方程即可求得集合A和集合B。
(![]() )讨论当集合A为
)讨论当集合A为![]() 和不为空集两种情况下B集合的关系,即可证明集合A与集合B的关系。
和不为空集两种情况下B集合的关系,即可证明集合A与集合B的关系。
(![]() )因为集合A为
)因为集合A为![]() ,所以分类讨论
,所以分类讨论![]() 与
与![]() 两种不同条件下B集合的情况,即可得到B集合也为
两种不同条件下B集合的情况,即可得到B集合也为![]() 。
。
(![]() )由
)由![]() ,
,
得![]() ,
,
解得![]() ,
,
由![]() ,得
,得![]() ,
,
解得![]() .
.
∴![]() ,
,![]() .
.
(![]() )若
)若![]() ,
,
则![]() 成立,
成立,
若![]() ,
,
设![]() 为
为![]() 中任意一个元素,
中任意一个元素,
则有![]() ,
,
∴![]() ,
,
故![]() ,
,
∴![]() .
.
(![]() )由
)由![]() ,得方程
,得方程![]() 无实数解,
无实数解,
∴![]() ,
,
①当![]() 时,
时,
![]() 的图象在
的图象在![]() 轴的上方,
轴的上方,
所以任意![]() ,
,![]() 恒成立,
恒成立,
即对于任意![]() ,
,
![]() 恒成立,
恒成立,
对于![]() ,则有
,则有![]() 成立,
成立,
∴对于![]() ,
,![]() 恒成立,
恒成立,
则![]() .
.
②当![]() 时,
时,
![]() 的图象在
的图象在![]() 轴的下方,
轴的下方,
所以任意![]() ,
,![]() 恒成立,
恒成立,
即对于![]() ,
,![]() 恒成立,
恒成立,
对于实数![]() ,则有
,则有![]() 成立,
成立,
所以对于任意![]() ,
,![]() 恒成立,
恒成立,
则![]() .
.
综上知,对于![]() ,
,
当![]() 时,
时,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c.设向量 ![]() =(a,c),
=(a,c), ![]() =(cosC,cosA).
=(cosC,cosA).
(1)若 ![]() ,c=
,c= ![]() a,求角A;
a,求角A;
(2)若 ![]() =3bsinB,cosA=
=3bsinB,cosA= ![]() ,求cosC的值.
,求cosC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
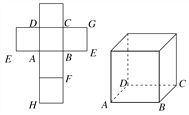
【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示.
(1)请按字母F、G、H标记在正方体相应地顶点处(不需要说明理由);
(2)判断平面BEG与平面ACH的位置关系.并说明你的结论;
(3)证明:直线DF⊥平面BEG.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,﹣2),椭圆E: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,F是椭圆的焦点,直线AF的斜率为
,F是椭圆的焦点,直线AF的斜率为 ![]() ,O为坐标原点.
,O为坐标原点.
(Ⅰ)求E的方程;
(Ⅱ)设过点A的直线l与E相交于P,Q两点,当△OPQ的面积最大时,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1g(1﹣x)的值域为(﹣∞,0),则函数f(x)的定义域为( )
A.[0,+∞]
B.(0,1)
C.[﹣9,+∞)
D.[﹣9,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品一年内出厂价格在6元的基础上按月份随正弦曲线波动,已知3月份达到最高价格8元,7月份价格最低为4元,该商品在商店内的销售价格在8元基础上按月份随正弦曲线波动,5月份销售价格最高为10元,9月份销售价最低为6元,假设商店每月购进这种商品m件,且当月销完,你估计哪个月份盈利最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com