如图，在斜三棱柱ABC－A1B1C1中，∠BAC＝90°，BC1⊥AC，则C1在底面ABC上的射影H必在( )
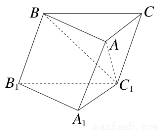
A．直线AB上 B．直线BC上
C．直线AC上 D．△ABC内部
科目：高中数学 来源：2015高考数学（理）一轮配套特训：8-3圆的方程（解析版） 题型：选择题
设圆的方程是x2＋y2＋2ax＋2y＋(a－1)2＝0，若0<a<1，则原点与圆的位置关系是( )
A．原点在圆上 B．原点在圆外
C．原点在圆内 D．不确定
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-7立体几何中的向量方法（解析版） 题型：填空题
如图，正方体ABCD－A1B1C1D1的棱长为1，E、F分别是棱BC、DD1上的点，如果B1E⊥平面ABF，则CE与DF的和的值为________．
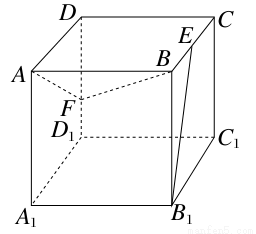
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-6空间向量及运算（解析版） 题型：选择题
已知平面α内有一个点A(2，－1,2)，α的一个法向量为n＝(3,1,2)，则下列点P中，在平面α内的是( )
A．(1，－1,1) B．(1,3，
)
C．(1，－3，
) D．(－1,3，－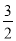
)
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-5直线、平面垂直的判定及性质（解析版） 题型：解答题
在如图所示的几何体中，AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD＝DE＝2AB，F为CD的中点．
(1)求证：AF∥平面BCE；
(2)求证：平面BCE⊥平面CDE.
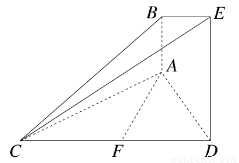
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-4直线、平面平行的判定及性质（解析版） 题型：解答题
直三棱柱ABC－A′B′C′，∠BAC＝90°，AB＝AC＝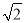
，AA′＝1，点M，N分别为A′B和B′C′的中点．
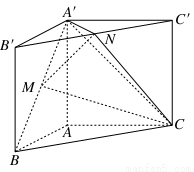
(1)证明：MN∥平面A′ACC′；
(2)求三棱锥A′－MNC的体积．(锥体体积公式V＝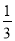
Sh，其中S为底面面积，h为高)
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-4直线、平面平行的判定及性质（解析版） 题型：填空题
设l，m，n表示不同的直线，α，β，γ表示不同的平面，给出下列四个命题：
①若m∥l，且m⊥α，则l⊥α；
②若m∥l，且m∥α，则l∥α；
③若α∩β＝l，β∩γ＝m，γ∩α＝n，则l∥m∥n；
④若α∩β＝m，β∩γ＝l，γ∩α＝n，且n∥β，则l∥m.
其中正确命题的个数是________．
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-3空间点直线平面之间的位置关系（解析版） 题型：选择题
如图，正方体ABCD－A′B′C′D′的棱长为4，动点E、F在棱AB上，且EF＝2，动点Q在棱D′C′上，则三棱锥A′－EFQ的体积( )
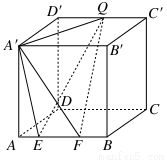
A．与点E、F的位置有关
B．与点Q的位置有关
C．与点E、F、Q的位置都有关
D．与点E、F、Q的位置均无关，是定值
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-6直接证明与间接证明（解析版） 题型：选择题
不相等的三个正数a、b、c成等差数列，并且x是a、b的等比中项，y是b、c的等比中项，则x2、b2、y2三数( )
A．成等比数列而非等差数列
B．成等差数列而非等比数列
C．既成等差数列又成等比数列
D．既非等差数列又非等比数列
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
