
【题目】将边长为正整数m、n的矩形划分成若干边长均为正整数的正方形,每个正方形的边均平行于矩形的相应边,试求这些正方形边长之和的最小值.

【答案】![]()
【解析】
记所求最小值为![]() ,可以证明
,可以证明![]() .(*)
.(*)
事实上,不妨设![]() .
.
(1)对m归纳,可证明存在一种合乎题意的分法,使所得正方形边长之和恰为![]() .
.
当m=1,时,命题显然成立.
假设当![]() 时,结论成立
时,结论成立![]() .当
.当![]() 时,若
时,若![]() ,则命题显然成立,若
,则命题显然成立,若![]() ,从矩形ABCD中切去正方形
,从矩形ABCD中切去正方形![]() (如图).由归纳假设,矩形
(如图).由归纳假设,矩形![]() 有一种分法使得所得正方形边长之和恰为
有一种分法使得所得正方形边长之和恰为![]() .
.
于是,原矩形ABCD有一种分法使得所得正方形边长之和为![]() .
.
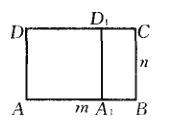
(2)对m归纳可以证明(*)成立.
当m=1时,由于n=1,显然![]() .
.
假设当![]() 时,对任意
时,对任意![]() ,有
,有![]() .
.
若![]() ,当
,当![]() 时,显然
时,显然![]()
当![]() 时,设矩形ABCD按要求分成了p个正方形,其边长分别为
时,设矩形ABCD按要求分成了p个正方形,其边长分别为![]() .不妨设
.不妨设![]() .
.
显然,![]() 或
或![]() .
.
若![]() ,则在AD与BC之间的与AD平行的任一直线至少穿过二个分成的正方形(或其边界),于是
,则在AD与BC之间的与AD平行的任一直线至少穿过二个分成的正方形(或其边界),于是![]() 不少于AB与CD之和.
不少于AB与CD之和.
故![]() .
.
若![]() ,则一个边长分别为m-n和n的矩形可按题目要求分成边长分别为
,则一个边长分别为m-n和n的矩形可按题目要求分成边长分别为![]() 的正方形,由归纳假设
的正方形,由归纳假设![]() .
.
从而,![]()
于是,当m=k+1时,![]()
再由(1)可知,![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某文体局为了解“跑团”每月跑步的平均里程,收集并整理了2018年1月至2018年11月期间“跑团”每月跑步的平均里程(单位:公里)的数据,绘制了下面的折线图.根据折线图,下列结论正确的是( )

A. 月跑步平均里程的中位数为6月份对应的里程数
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在8、9月
D. 1月至5月的月跑步平均里程相对于6月至11月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() .
.
(1) 若不等式k≤xf(x)+![]() 在x∈[1,3]上恒成立,求实数k的取值范围;
在x∈[1,3]上恒成立,求实数k的取值范围;
(2) 当x∈![]() (m>0,n>0)时,函数g(x)=tf(x)+1(t≥0)的值域为[2-3m,2-3n],求实数t的取值范围.
(m>0,n>0)时,函数g(x)=tf(x)+1(t≥0)的值域为[2-3m,2-3n],求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设曲线![]() (a为正常数)与
(a为正常数)与![]() 在x轴上方仅有一个公共点P.
在x轴上方仅有一个公共点P.
(1)求实数m的取值范围(用a表示);
(2)O为原点,若![]() 与x轴的负半轴交于点A,当
与x轴的负半轴交于点A,当![]() 时,试求△OAP的面积的最大值(用a表示).
时,试求△OAP的面积的最大值(用a表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 a ∈ N+ , a ≥ 2 , 集合![]() .在闭区间[ 1, a ] 上是否存在 b , 使 A ∩ B ≠
.在闭区间[ 1, a ] 上是否存在 b , 使 A ∩ B ≠ ![]() ? 如果存在, 求出 b 的一切可能值及相应的 A ∩ B;如果不存在, 试说明理由.
? 如果存在, 求出 b 的一切可能值及相应的 A ∩ B;如果不存在, 试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在古装电视剧《知否》中,甲乙两人进行一种投壶比赛,比赛投中得分情况分“有初”“贯耳”“散射”“双耳”“依竿”五种,其中“有初”算“两筹”,“贯耳”算“四筹”,“散射”算“五筹”,“双耳”算“六筹”,“依竿”算“十筹”,三场比赛得筹数最多者获胜.假设甲投中“有初”的概率为![]() ,投中“贯耳”的概率为
,投中“贯耳”的概率为![]() ,投中“散射”的概率为
,投中“散射”的概率为![]() ,投中“双耳”的概率为
,投中“双耳”的概率为![]() ,投中“依竿”的概率为
,投中“依竿”的概率为![]() ,乙的投掷水平与甲相同,且甲乙投掷相互独立.比赛第一场,两人平局;第二场,甲投了个“贯耳”,乙投了个“双耳”,则三场比赛结束时,甲获胜的概率为( )
,乙的投掷水平与甲相同,且甲乙投掷相互独立.比赛第一场,两人平局;第二场,甲投了个“贯耳”,乙投了个“双耳”,则三场比赛结束时,甲获胜的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为
,短轴长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若椭圆![]() 的左焦点为
的左焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,则在
两点,则在![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() 使得直线
使得直线![]() 的斜率互为相反数?若存在,求出定点
的斜率互为相反数?若存在,求出定点![]() 的坐标;若不存在,也请说明理由.
的坐标;若不存在,也请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△![]() 的三个内角
的三个内角![]() 、
、![]() 、
、![]() 所对应的边分别为
所对应的边分别为![]() 、
、![]() 、
、![]() ,复数
,复数![]() ,
,![]() ,(其中
,(其中![]() 是虚数单位),且
是虚数单位),且![]() .
.
(1)求证:![]() ,并求边长
,并求边长![]() 的值;
的值;
(2)判断△![]() 的形状,并求当
的形状,并求当![]() 时,角
时,角![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com