
| A. | {x|x<0或1<x<2} | B. | {x|-2<x<-1或x>0} | C. | {x|x<-2或-1<x<0} | D. | {x|0<x<1或x>2} |
分析 根据函数为奇函数求出f(-1)=0,再将不等式f(x+1)<0分成两类加以讨论,再分别利用函数的单调性进行求解,可以得出相应的解集再求并即可.
解答 解:∵f(x)为奇函数,且在(0,+∞)上是增函数,f(1)=0,
∴f(-1)=-f(1)=0,且函数f(x)在(-∞,0)内是增函数.
∴f(x+1)<0?当x+1>0时,f(x+1)<0=f(1)或
当x+1<0时,f(x+1)<0=f(-1)
根据f(x)在(-∞,0)和(0,+∞)内是都是增函数,
得到:0<x+1<1或x+1<-1⇒-1<x<0或x<-2
故选:C.
点评 本题主要考查了函数的奇偶性的性质,以及函数单调性的应用等有关知识,属于基础题.结合函数的草图,会对此题有更深刻的理解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{39}{7}$ | B. | $\frac{17}{3}$ | C. | $\frac{71}{13}$ | D. | $\frac{31}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 90°<A<180° | B. | 45°<A<90° | C. | 60°<A<90° | D. | 0°<A<90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1000×(1+5×5%)万元 | B. | 1000×(1+5%)5万元 | ||
| C. | $1000×\frac{{1.05×(1-{{1.05}^4})}}{1-1.05}万元$ | D. | $1000×\frac{{1.05×(1-{{1.05}^2})}}{1-1.05}万元$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
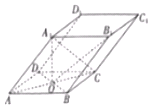 如图,四棱柱ABCD-A1B1C1D1的底面AB是CD菱形,AC∩BD=O,A1O⊥底面ABCD,AB=AA1=2.
如图,四棱柱ABCD-A1B1C1D1的底面AB是CD菱形,AC∩BD=O,A1O⊥底面ABCD,AB=AA1=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com