
分析 (1)求解出集合A,集合B,根据集合的基本运算求(∁RA)∪B;
(2)根据(a,a+1)⊆B,求a的取值范围
解答 解析:(1)集合A={x|log2(x2-2x-8)<4},
由log2(x2-2x-8)<4得:0<x2-2x-8<16,即$\left\{\begin{array}{l}(x+2)(x-4)>0\\(x+4)(x-6)<0\end{array}\right.$,
解得:-4<x<-2或4<x<6,
∴集合A=(-4,-2)∪(4,6).
那么:∁RA=(-∞-4]∪[-2,4]∪[6,+∞),
集合B={x|$\frac{1}{4}$<2${\;}^{{x^2}-x}}$<64}.
由$\frac{1}{4}$<${2^{{x^2}-3}}$<64
可得:2-2<${2^{{x^2}-3}}$<26,即-2<x2-3<6,
化简得:1<x2<9,
解得:-3<x<-1或1<x<3,
∴集合B=(-3,-1)∪(1,3),
所以:(∁RA)∪B=(-∞-4]∪(-3,4]∪[6,+∞).
(2)由(1)可知集合B=(-3,-1)∪(1,3),
当(a,a+1)⊆B时,满足$\left\{\begin{array}{l}-3≤a\\ a+1≤-1\end{array}\right.$或$\left\{\begin{array}{l}1≤a\\ a+1≤3\end{array}\right.$,
解得:-3≤a≤-2或1≤a≤2
所以a的取值范围是[-3,-2]∪[1,2].
点评 本题考查了对数的计算和指数的计算能力和集合的基本运算,比较基础.属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
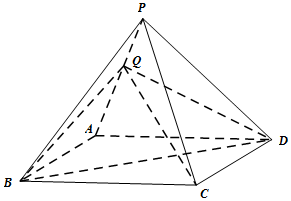 如图所示,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,Q是棱PA上的动点.
如图所示,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,Q是棱PA上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<0或1<x<2} | B. | {x|-2<x<-1或x>0} | C. | {x|x<-2或-1<x<0} | D. | {x|0<x<1或x>2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com