
分析 (1)由f(1-x)=f(1+x),得到对称轴为x=1,即可求出a的值,
(2)根据二次函数的性质,分类讨论即可求出g(a),再根据奇偶性的定义即可判断.
解答 解:(1)∵函数f(x)=x2+2ax+a2-1对任意的实数x都有f(1+x)=f(1-x)成立,
∴函数的对称轴x=-a=1,
∴a=-1,
(2)∵f(x)=x2+2ax+a2-1=(x+a)2-1,其对称轴为x=-a,
当-a≤-1时,即a≥1时,函数f(x)在[-1,1]上单调递增,故g(a)=f(x)min=f(-1)=a2-2a,
当-1<-a<1时,即-1<a<1时,故g(a)=f(x)min=f(a)=-1,
当-a≥1时,即a≤-1时,函数f(x)在[-1,1]上单调递减,故g(a)=f(x)min=f(1)=a2+2a,
∴g(a)=$\left\{\begin{array}{l}{{a}^{2}-2a,a≥1}\\{-1,-1<a<1}\\{{a}^{2}+2a,a≤-1}\end{array}\right.$,
∵g(-a)=g(a),
∴g(a)为偶函数
点评 本题考查函数的单调性与奇偶性,考查分类讨论的数学思想,属于中档题


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 身高/cm | 170 | 168 | 178 | 168 | 176 | 172 |
| 体重/kg | 65 | 64 | 72 | 61 | 67 | 67 |
| A. | 80 kg | B. | 71.6 kg | C. | 68.4 kg | D. | 64.8 kg |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
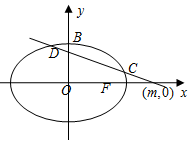 如图,已知圆G:x2+y2-2x-$\sqrt{2}$y=0经过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为$\frac{5}{6}$π的直线l交椭圆于C,D两点.
如图,已知圆G:x2+y2-2x-$\sqrt{2}$y=0经过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为$\frac{5}{6}$π的直线l交椭圆于C,D两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6$\sqrt{3}$ | B. | 6 | C. | 12 | D. | 12$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com