
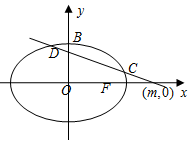
 如图,已知圆G:x2+y2-2x-$\sqrt{2}$y=0经过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为$\frac{5}{6}$π的直线l交椭圆于C,D两点.
如图,已知圆G:x2+y2-2x-$\sqrt{2}$y=0经过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为$\frac{5}{6}$π的直线l交椭圆于C,D两点.分析 (I)圆G:x2+y2-2x-$\sqrt{2}$y=0,分别令y=0,x=0,解出可得椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F,上顶点B,可得c,b,a2=b2+c2,即可得出.
(II)设C(x1,y1),D(x2,y2),直线l的方程为:y=$-\frac{\sqrt{3}}{3}$(x-m),与椭圆方程联立化为:6y2-2$\sqrt{3}$my+m2-6=0,△>0,解得m2<12.由FC⊥FD,可得$\overrightarrow{FC}•\overrightarrow{FD}$=(x1-2)(x2-2)+y1y2=$(m+\sqrt{3}{y}_{1}-2)$$(m+\sqrt{3}{y}_{2}-2)$+y1y2=0,把根与系数的关系代入解出m即可得出.
解答 解:(I)圆G:x2+y2-2x-$\sqrt{2}$y=0,令y=0,可得x2-2x=0,解得x=2,或0(舍去).
令x=0,可得y2-$\sqrt{2}$y=0,解得y=$\sqrt{2}$,或0(舍去).
∴椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F(2,0),上顶点B$(0,\sqrt{2})$,
∴c=2,b=$\sqrt{2}$,a2=b2+c2=6,
可得椭圆的方程为$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}$=1.
(II)设C(x1,y1),D(x2,y2),
直线l的方程为:y=$-\frac{\sqrt{3}}{3}$(x-m),
联立$\left\{\begin{array}{l}{\sqrt{3}y+x-m=0}\\{\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,化为:6y2-2$\sqrt{3}$my+m2-6=0,
△=12m2-24(m2-6)>0,解得m2<12.
∴y1+y2=$\frac{\sqrt{3}m}{3}$,y1•y2=$\frac{{m}^{2}-6}{6}$.
∵FC⊥FD,∴$\overrightarrow{FC}•\overrightarrow{FD}$=(x1-2)(x2-2)+y1y2=$(m-\sqrt{3}{y}_{1}-2)$$(m-\sqrt{3}{y}_{2}-2)$+y1y2=0,
∴-$\sqrt{3}$(m-2)(y1+y2)+4y1•y2+(m-2)2=0,
∴-$\sqrt{3}$(m-2)×$\frac{\sqrt{3}m}{3}$+4×$\frac{{m}^{2}-6}{6}$+(m-2)2=0,
化为:m2-3m=0,m$>\sqrt{6}$,m2<12,解得m=3.
∴m=3.
点评 本题考查了直线与椭圆线相交问题、一元二次方程的根与系数的关系、数量积运算性质、不等式的解法,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{3}$,1) | B. | ($\frac{1}{3}$,$\frac{1}{2}$) | C. | ($\frac{1}{3}$,$\frac{5}{8}$) | D. | ($\frac{5}{8}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.6826 | B. | 0.3174 | C. | 0.9544 | D. | 0.9974 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
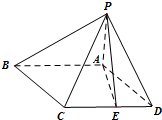 如图,四棱锥P-ABCD的底面ABCD是菱形,PA⊥AB,PC=PD,E是CD的中点.
如图,四棱锥P-ABCD的底面ABCD是菱形,PA⊥AB,PC=PD,E是CD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com