
分析 (1)f(x)在x=-2时有极值,且在x=-1处的切线的斜率为-3,可有:$\left\{\begin{array}{l}{f'(-2)=0}\\{f'(-1)=-3}\end{array}\right.$⇒$\left\{\begin{array}{l}{b=3}\\{c=0}\end{array}\right.$;
(2)函数f(x)的解析式为:f(x)=x3+3x2-1,利用导数判断出函数的单调区间,求出极值;
(3)过点P(1,m)可作曲线y=f(x)的三条切线,即存在三个x0,也即是y=m与h(x)=-2${x}_{0}^{3}$+6x0-1有三个交点.
解答 解:(1)f'(x)=3x2+2bx+c
f(x)在x=-2时有极值,且在x=-1处的切线的斜率为-3
可有:$\left\{\begin{array}{l}{f'(-2)=0}\\{f'(-1)=-3}\end{array}\right.$⇒$\left\{\begin{array}{l}{b=3}\\{c=0}\end{array}\right.$
函数f(x)的解析式为:f(x)=x3+3x2-1
(2)由(1)知:f'(x)=3x2+6x
令f'(x)=0,有x1=0,x2=-2.
所以,当x∈[-1,0]时,f'(x)<0,f(x)在(-1,0)上单调递减;
当x∈[0,2]时,f'(x)>0,f(x)在(0,2)上单调递增;
∴f(x)min=f(0)=-1;f(x)max=max{f(-1),f(2)}=f(2)=19.
(3)设切点为(x0,${x}_{0}^{3}$+3${x}_{0}^{2}$-1)
切线斜率为:k=f'(x0)=3${x}_{0}^{2}$+6x0
∴切线方程为:y-(${x}_{0}^{3}$+3${x}_{0}^{2}$-1)=(3${x}_{0}^{2}$+6x0)(x-x0) ①
又切线过点P(1,m),带入①化简为:m=-2${x}_{0}^{3}$+6x0-1
令y=m 与 h(x0)=-2${x}_{0}^{3}$+6x0-1
h(-1)=-5,h(1)=3,h(0)=-1;
h'(x0)=-6${x}_{0}^{2}$+6,令h'(x0)=0⇒x1=-1,x2=1;
h(x0)在(-∞,-1),(1,+∞)单调递减,(-1,1)上单调递增;
过点P(1,m)可作曲线y=f(x)的三条切线,即存在三个x0,也即是y=m与h(x)有三个交点.
故如图所知:-5<m<3.
点评 本题主要考查了导数与切线方程,函数极值,函数的单调性以及函数与方程思想,属中等题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在(0,+∞)上是减函数 | B. | 在(0,+∞)上是增函数 | ||
| C. | 在(1,+∞)上是减函数 | D. | 在(1,+∞)上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)={x^3}\;g(x)=\root{3}{x^9}$ | B. | $f(x)={x^2}\;g(x)={(\sqrt{x})^4}$ | C. | f(x)=1g(x)=x0 | D. | $f(x)=x\;g(x)=\frac{x^2}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
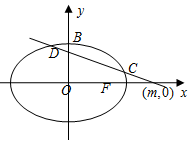 如图,已知圆G:x2+y2-2x-$\sqrt{2}$y=0经过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为$\frac{5}{6}$π的直线l交椭圆于C,D两点.
如图,已知圆G:x2+y2-2x-$\sqrt{2}$y=0经过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为$\frac{5}{6}$π的直线l交椭圆于C,D两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
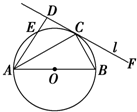 如图所示,⊙O的直径为6,AB为⊙O的直径,C为圆周上一点,BC=3,过C作圆的
如图所示,⊙O的直径为6,AB为⊙O的直径,C为圆周上一点,BC=3,过C作圆的查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com