
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 以OB,OC为邻边作平行四边形OBFC,连接OF与 BC相交于点E,E为BC的中点.2$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$,可得$\overrightarrow{OB}+\overrightarrow{OC}$=-2$\overrightarrow{OA}$=$\overrightarrow{OF}$=2$\overrightarrow{OE}$,因此点O是直线AE的中点.可得B,O,D三点共线,$\overrightarrow{AD}$=t$\overrightarrow{AC}$,∴点D是BO与AC的交点.过点O作OM∥BC交AC于点M,点M为AC的中点.利用平行线的性质即可得出.
解答 解:以OB,OC为邻边作平行四边形OBFC,连接OF与 BC相交于点E,E为BC的中点.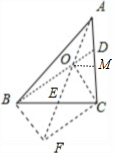
∵2$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$,∴$\overrightarrow{OB}+\overrightarrow{OC}$=-2$\overrightarrow{OA}$=$\overrightarrow{OF}$=2$\overrightarrow{OE}$,
∴点O是直线AE的中点.
∵B,O,D三点共线,$\overrightarrow{AD}$=t$\overrightarrow{AC}$,∴点D是BO与AC的交点.
过点O作OM∥BC交AC于点M,则点M为AC的中点.
则OM=$\frac{1}{2}$EC=$\frac{1}{4}$BC,
∴$\frac{DM}{DC}$=$\frac{1}{4}$,
∴$DM=\frac{1}{3}MC$,
∴AD=$\frac{2}{3}$AM=$\frac{1}{3}$AC,$\overrightarrow{AD}$=t$\overrightarrow{AC}$,
∴t=$\frac{1}{3}$.
另解:由2$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$,∴点O是直线AE的中点.
∵B,O,D三点共线,∴存在实数k使得$\overrightarrow{AO}$=k$\overrightarrow{AB}$+(1-k)$\overrightarrow{AD}$=k$\overrightarrow{AB}$+(1-k)t$\overrightarrow{AC}$=$\frac{1}{4}$$(\overrightarrow{AB}+\overrightarrow{AC})$,
∴k=$\frac{1}{4}$,(1-k)t=$\frac{1}{4}$,解得t=$\frac{1}{3}$.
故选:B.
点评 本题考查了向量三角形法则、平行线的性质定理、向量共线定理三角形中位线定理,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $a+\frac{1}{a}$的最小值是2 | B. | ${a^2}+\frac{1}{a^2}$的最小值是2 | ||
| C. | $a+\frac{1}{a}$的最大值是2 | D. | ${a^2}+\frac{1}{a^2}$的最大值是2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-1)>f($\frac{π}{3}$)>f(-π) | B. | f($\frac{π}{3}$)>f(-1)>f(-π) | C. | f(-π)>f($\frac{π}{3}$)>f(-1) | D. | f(-1)>f(-π)>f($\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.6826 | B. | 0.3174 | C. | 0.9544 | D. | 0.9974 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com