
分析 (Ⅰ)由a1=2,a2=3,结合lgan+1=|lgan-lgan-1|(n=2,3,4,…)可得a3,a4,a5的值;
(Ⅱ)分必要性和充分性证明,充分性利用反证法证明;
(Ⅲ)利用反证法,假设数列{an}中不存在ak(k∈N*),使得1≤ak<2,则0<ak<1或ak≥2(k=1,2,3,…).然后分类推出矛盾得答案.
解答 (Ⅰ)解:∵a1=2,a2=3,lgan+1=|lgan-lgan-1|(n=2,3,4,…),
∴lga3=|lg3-lg2|=$lg\frac{3}{2}$,即${a}_{3}=\frac{3}{2}$;
$lg{a}_{4}=|lg\frac{3}{2}-lg3|=lg2$,即a4=2;
$lg{a}_{5}=|lg2-lg\frac{3}{2}|=lg\frac{4}{3}$,即${a}_{5}=\frac{4}{3}$;
(Ⅱ)证明:必要性、已知数列{an}中有无数多项是1,则数列{an}中存在ak(k∈N*)使得lgak=0.
∵数列{an}中有无数多项是1,∴数列{an}中存在ak(k∈N*)使得ak=1,
即数列{an}中存在ak(k∈N*)使得lgak=0.
充分性:已知数列{an}中存在ak(k∈N*)使得lgak=0,则数列{an}中有无数多项是1.
假设数列{an}中没有无数多项是1,不妨设${a}_{m}=1(m∈{N}^{*})$是数列{an}中为1的最后一项,则am+1≠1,
若am+1>1,则由lgan+1=|lgan-lgan-1|(n=2,3,4,…),可得lgam+2=lgam+1,
∴lgam+3=|lgam+2-lgam+1|=0,则lgam+3=1,与假设矛盾;
若0<am+1<0,则由lgan+1=|lgan-lgan-1|(n=2,3,4,…),可得lgam+2=-lgam+1,
∴lgam+3=|lgam+2-lgam+1|=-2lgam+1,
lgam+4=|lgam+3-lgam+2|=|-2lgam+1+lgam+1|=-lgam+1,
lgam+5=|lgam+4-lgam+3|=|-lgam+1+2lgam+1|=-lgam+1,
∴lgam+6=|lgam+5-lgam+4|=0,得lgam+6=1,与假设矛盾.
综上,假设不成立,原命题正确;
(Ⅲ)证明:假设数列{an}中不存在ak(k∈N*),使得1≤ak<2,
则0<ak<1或ak≥2(k=1,2,3,…).
由lgan+1=|lgan-lgan-1|(n=2,3,4,…),可得
${a}_{n+1}=\left\{\begin{array}{l}{\frac{{a}_{n}}{{a}_{n-1}},{a}_{n}≥{a}_{n-1}}\\{\frac{{a}_{n-1}}{{a}_{n}},{a}_{n}<{a}_{n-1}}\end{array}\right.$(n=1,2,3,…)*,且an>0(n=1,2,3,…),
∴当n≥2时,an≥1,an≥2(n=3,4,5,…).
若a4=a3≥2,则a5=1,与a5≥2矛盾;
若a4≠a3≥2,
设bm=max{a2m+1,a2m+2}(m=1,2,3,…),则bm≥2.
由(*)可得,${a}_{2m+3}≤\frac{max\{{a}_{2m+1},{a}_{2m+2}\}}{2}=\frac{1}{2}{b}_{m}$,
${a}_{2m+4}≤\frac{1}{2}max\{{a}_{2m+2},{a}_{2m+3}\}$,
∴$max\{{a}_{2m+3},{a}_{2m+4}\}≤\frac{1}{2}{b}_{m}$,即${b}_{m+1}≤\frac{1}{2}{b}_{m}$(m=1,2,3,…),
∴${b}_{m}≤\frac{{b}_{1}}{{2}^{m+1}}$,
对于b1,显然存在l使得${2}^{l-1}≤{b}_{l}<{2}^{l}$.
∴${b}_{l+1}≤\frac{{b}_{1}}{{2}^{l}}<1$,这与bm≥2矛盾.
∴假设不成立,原命题正确.
点评 本题考查数列递推式,考查了充分必要条件的判定,体现了分类讨论的数学思想方法,考查逻辑思维能力与推理论证能力,训练了反证法证题的方法,属难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
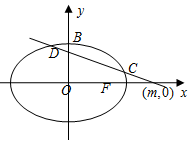 如图,已知圆G:x2+y2-2x-$\sqrt{2}$y=0经过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为$\frac{5}{6}$π的直线l交椭圆于C,D两点.
如图,已知圆G:x2+y2-2x-$\sqrt{2}$y=0经过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为$\frac{5}{6}$π的直线l交椭圆于C,D两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com