
分析 利用三棱锥P-ABC的内切球的球心,将三棱锥分割成3个三棱锥,利用等体积,即可求得结论.
解答 解:由题意,设三棱锥P-ABC的内切球的半径为r,球心为O,则由等体积
VB-PAC=VO-PAB+VO-PAC+VO-ABC
可得$\frac{1}{3}×\frac{1}{2}×2×1×1$=$\frac{1}{3}×\frac{1}{2}×2×1×2×r$+$\frac{1}{3}×\frac{1}{2}×1×1×r$+$\frac{1}{3}×\frac{1}{2}×\sqrt{2}×\sqrt{5-\frac{1}{2}}×r$,
∴r=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查三棱锥P-ABC的内切球,考查学生分析转化问题的能力,正确求体积是关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:解答题
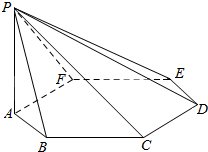 设ABCDEF是边长为1的正六边形,PA垂直于正六边形所在的平面,且PA=2.求
设ABCDEF是边长为1的正六边形,PA垂直于正六边形所在的平面,且PA=2.求查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com