
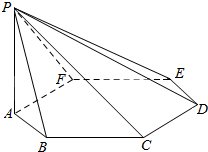
 设ABCDEF是边长为1的正六边形,PA垂直于正六边形所在的平面,且PA=2.求
设ABCDEF是边长为1的正六边形,PA垂直于正六边形所在的平面,且PA=2.求分析 根据根据距离的定义以及空间角的求解分别进行计算即可.
解答 解:(1)连接AC,在正六边形中,AC⊥CD,
∵PA垂直于正六边形所在的平面,
∴PA⊥CD,则CD⊥平面PAC,
则CD⊥PC,即点P到直线CD的距离为PC,
∵ABCDEF是边长为1的正六边形,PA=2,
∴AD=2,AC=$\sqrt{A{D}^{2}-C{D}^{2}}$=$\sqrt{{2}^{2}-1}=\sqrt{3}$.
则PC=$\sqrt{P{A}^{2}+A{C}^{2}}$=$\sqrt{1+3}=\sqrt{4}$=2,
(2)∵BC∥AD,BC?平面PAD,AD?平面PAD,
∴BC∥平面PAD,
过B作BM⊥AD,
则BM是直线BC与平面PAD的距离,
则BM=$\frac{\sqrt{3}}{2}$.
(3)∵BD⊥PA,
∴BD⊥面PAB,
过A作AN⊥PB,则AN⊥面PBD,
即AN是点A到平面PBD的距离,
△PAB中,PA=2,AB=1,PB=$\sqrt{5}$,
则AN•PB=PA•AB,即AN=$\frac{PA•AB}{PB}=\frac{2×1}{\sqrt{5}}=\frac{2\sqrt{5}}{5}$.
(4)∵CD∥BE,
∴BE与PE所成的角就是异面直线CD与PE所成的角,
∵BE=2,PB=$\sqrt{5}$,
∴tan∠PEB=$\frac{PB}{BE}$=$\frac{\sqrt{5}}{2}$,即∠PEB=arctan$\frac{\sqrt{5}}{2}$.
即异面直线CD与PE所成的角为arctan$\frac{\sqrt{5}}{2}$.
(5)∵BD⊥AB,PA⊥BD,
∴BD⊥面PAB,
则PB是PD在平面PAB上的射影,
则∠DPB是直线PD与平面PAB所成的角,
∵PB=$\sqrt{5}$,BD=$\sqrt{3}$,
∴tan∠DPB=$\frac{BD}{PB}$=$\frac{\sqrt{3}}{\sqrt{5}}$=$\frac{\sqrt{13}}{5}$,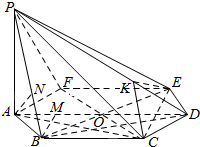
则∠DPB=arctan$\frac{\sqrt{13}}{5}$.
(6)∵△PCD≌△PDE,
∴过C作CK⊥PD,连接KE,
则KE⊥PD,
则∠CKE是二面角C-PD-E的平面角,
∵CD⊥AC,PA⊥CD,
∴CD⊥面PAC,则CD⊥PC,
则PC=$\sqrt{P{A}^{2}+A{C}^{2}}$=$\sqrt{{2}^{2}+(\sqrt{3})^{2}}$=$\sqrt{7}$,PD=$\sqrt{P{A}^{2}+A{D}^{2}}=\sqrt{4+4}$=2$\sqrt{2}$,
则CD•PC=PD•CK,
即CK=$\frac{CD•PC}{PD}$=$\frac{1×\sqrt{7}}{2\sqrt{2}}$=$\frac{\sqrt{14}}{4}$,
则KE=CK=$\frac{\sqrt{14}}{4}$,
在△CKE中,cos∠CKE=$\frac{C{K}^{2}+K{E}^{2}-C{E}^{2}}{2CK•KE}$=$\frac{(\frac{\sqrt{14}}{4})^{2}+(\frac{\sqrt{14}}{4})^{2}-(\sqrt{3})^{2}}{2×\frac{\sqrt{14}}{4}×\frac{\sqrt{14}}{4}}$=$-\frac{5}{7}$,
即∠CKE=arccos($-\frac{5}{7}$).
点评 本题主要考查空间距离的计算以及空间角的求解,根据相应的定义进行是解决本题的关键.综合性较强,运算量较大.


科目:高中数学 来源: 题型:解答题
 已知平面五边形ADCEF关于BC对称,点B在AF上(如图1),DE与BC交于点G,且AD=AB=1,CD=BC=$\sqrt{3}$,将此图形沿BC折叠成直二面角,连接AF,DE得到几何体(如图2).
已知平面五边形ADCEF关于BC对称,点B在AF上(如图1),DE与BC交于点G,且AD=AB=1,CD=BC=$\sqrt{3}$,将此图形沿BC折叠成直二面角,连接AF,DE得到几何体(如图2).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com