
分析 根据f(x+2)=-f(x)便可得到f(x)是周期为4的周期函数,从而可以得出f(2015)+f(2016)=f(-1)+f(0),而根据f(x)为奇函数便可求出f(-1)=-2,f(0)=0,这样即可得出f(2015)+f(2016)的值.
解答 解:f(x)=-f(x+2)=f(x+4);
∴f(x)是周期为4的周期函数;
∴f(2015)+f(2016)=f(-1+504×4)+f(0+504×4)=f(-1)+f(0);
∵f(x)是奇函数;
∴f(0)=0,f(-1)=-f(1)=-2;
∴f(2015)+f(2016)=-2.
故答案为:-2.
点评 考查周期函数的定义,以及奇函数的定义,奇函数在原点有定义时,原点处的函数值为0.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{y^2}{2}-\frac{x^2}{8}=1$ | B. | $\frac{y^2}{8}-\frac{x^2}{2}=1$ | C. | $\frac{y^2}{2}-\frac{x^2}{4}=1$ | D. | $\frac{y^2}{4}-\frac{x^2}{2}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥A-BCD中,平面ABD和底面BCD垂直,点F是棱CD上的动点,E,O分别是AD,BD的中点,已知AB=AD=$\sqrt{2}$,BD=2CD,∠BAD=∠BDC=90°.
如图,在三棱锥A-BCD中,平面ABD和底面BCD垂直,点F是棱CD上的动点,E,O分别是AD,BD的中点,已知AB=AD=$\sqrt{2}$,BD=2CD,∠BAD=∠BDC=90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 90° | C. | 120° | D. | 135° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
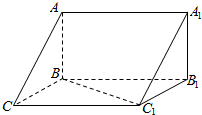 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,BC=1,CC1=2,BC1=$\sqrt{3}$.
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,BC=1,CC1=2,BC1=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| f(x) | 11.8 | 8.6 | -6.4 | 4.5 | -26.8 | -86.2 |
| A. | 2个 | B. | 3个 | C. | 至少3个 | D. | 至多2个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
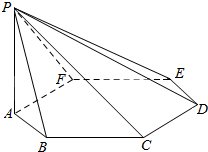 设ABCDEF是边长为1的正六边形,PA垂直于正六边形所在的平面,且PA=2.求
设ABCDEF是边长为1的正六边形,PA垂直于正六边形所在的平面,且PA=2.求查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com