
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | 1 | D. | $\frac{5}{2}$ |
分析 由复数代数形式的乘除运算化简复数z,求出$\overline{z}$,然后代入z•$\overline{z}$计算得答案.
解答 解:由z=$\frac{1-2i}{1+i}$=$\frac{(1-2i)(1-i)}{(1+i)(1-i)}=\frac{-1-3i}{2}=-\frac{1}{2}-\frac{3}{2}i$,
得$\overline{z}=-\frac{1}{2}+\frac{3}{2}i$,
则z•$\overline{z}$=$(-\frac{1}{2}-\frac{3}{2}i)•(-\frac{1}{2}+\frac{3}{2}i)=\frac{5}{2}$.
故选:D.
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 30 | 40 | 50 | 60 |
| y | 25 | 30 | 40 | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -200 | B. | -100 | C. | 0 | D. | -50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 回归直线过样本点的中心($\overline{x}$,$\overline{y}$) | |
| B. | 两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1 | |
| C. | 在回归直线方程$\stackrel{∧}{y}$=0.2x+0.8中,当解释变量x每增加1个单位时,预报变量$\stackrel{∧}{y}$平均增加0.2个单位 | |
| D. | 对分类变量X与Y,随机变量K2的观测值k越大,则判断“X与Y有关系”的把握程度越小 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{5}$ | B. | -$\frac{12}{5}$ | C. | $\frac{5}{12}$ | D. | -$\frac{5}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
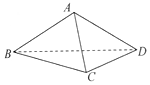 如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,该三棱锥三视图的正视图为( )
如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,该三棱锥三视图的正视图为( )| A. |  | B. | 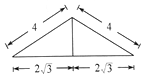 | C. | 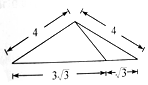 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com